Chứng minh rằng: 281+255 chia hết cho 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
1^10-1=(11-1)(11^9+11^8+...+11+1)=10(11...
11^x-1 chia het cho 10 voi moi x
suy ra: 11^9+11^8+...+11+1-10 chia het cho 10
suy ra 11^9+11^8+...+11+1 chia het cho 10
suy ra 11^10-1 chia het cho 100
1^10-1=(11-1)(11^9+11^8+...+11+1)=10(11...
11^x-1 chia het cho 10 voi moi x
suy ra: 11^9+11^8+...+11+1-10 chia het cho 10
suy ra 11^9+11^8+...+11+1 chia het cho 10
suy ra 11^10-1 chia het cho 100

a) Ta thấy \(999993^{1999}⋮̸5\) và \(55555^{1997}⋮5\) nên \(999993^{1999}-55555^{1997}⋮̸5\), mâu thuẫn đề bài.
b)
Ta có \(17^{25}=17^{4.6+1}=17.\left(17^4\right)^6=17.\overline{A1}=\overline{B7}\) có chữ số tận cùng là 7. \(13^{21}=13^{4.5+1}=13.\left(13^4\right)^5=13.\overline{C1}=\overline{D3}\) có chữ số tận cùng là 3. \(24^4=4^4.6^4=\overline{E6}.\overline{F6}=\overline{G6}\) có chữ số tận cùng là 6 nên \(17^{25}-13^{21}+24^4\) có chữ số tận cùng là chữ số tận cùng của \(7-3+6=10\) hay là 0. Vậy \(17^{25}-13^{21}+24^4⋮10\)
c) Cách làm tương tự câu b.

Bài 1 :
abc chia hết cho 27
\(\Rightarrow\)100a + 10b + c chia hết cho 27
\(\Rightarrow\)10(100a + 10b + c) chia hết cho 27
\(\Rightarrow\)1000a + 100b + 10c chia hết cho 27
\(\Rightarrow\)999a + (100b + 10c + a) chia hết cho 27
Mà 999a chia hết cho 27
Vậy 100b + 10c + a = bca chia hết cho 27
Bài 2 :
a) ab + ba = 10a + b + 10b + a = (10a + a) + (10b + b) = 11a + 11b = 11(a + b) chia hết cho 11
b)Ta thấy ab và ba có tổng các chữ số như nhau nên có cùng số dư khi chia cho 9, do đó hiệu của chúng phải chia hết cho 9
abc chia hết cho 27
=100a+10b+10c chia hết cho 27
=10(100a+10b+c) chia hết cho 27
=1000a+100b+10c chia hết cho 27
=999a+(100b+10c+a) chia hết cho 27
Mà 999a chia hết cho 27
Vậy 100b+10c+a=bca chia hết cho 27

A = 10ⁿ + 72n - 1 = 10ⁿ - 1 + 72n
10ⁿ - 1 = 99...9 (có n-1 chữ số 9) = 9x(11..1) (có n chữ số 1)
A = 10ⁿ - 1 + 72n = 9x(11...1) + 72n => A : 9 = 11..1 + 8n = 11...1 -n + 9n
thấy 11...1 có n chữ số 1 có tổng các chữ số là n => 11..1 - n chia hết cho 9
=> A : 9 = 11..1 - n + 9n chia hết cho 9
=> A chia hết cho 81
k mình nha bạn

a. VD: (12 + 30 + 68) \(⋮\)11 nên 123068 \(⋮\)11
Vậy: (ab + cd + eg) \(⋮\)11 thì abcdeg \(⋮\)11.
b. Đề bài sai
Chúc bạn học tốt!

taco;17achia het cho17
suy ra 17a+3a+2b chia het cho17
suy ra20a+2bchia het cho17
rút gọn cho 2
suyra 10a+b chia hết cho 17


Bài 5:
b: Ta có: \(n+6⋮n+2\)
\(\Leftrightarrow n+2\in\left\{2;4\right\}\)
hay \(n\in\left\{0;2\right\}\)
c: Ta có: \(3n+1⋮n-2\)
\(\Leftrightarrow n-2\in\left\{-1;1;7\right\}\)
hay \(n\in\left\{1;3;9\right\}\)
Ta có:
\(2^{81}+2^{55}\)
\(=2^{80}.2+2^{52}.2^3\)
\(=\left(2^4\right)^{20}.2+\left(2^4\right)^{13}.8\)
\(=\overline{\left(...6\right)}^{20}.2+\overline{\left(...6\right)}^{13}.8\)
\(=\overline{\left(...6\right)}.2+\overline{\left(...6\right)}.8\)
\(=\overline{...2}+\overline{...8}\)
\(=\overline{...0}\)
Vì \(\overline{...0}⋮10\) nên \(2^{81}+2^{55}⋮10\)
Vậy \(2^{81}+2^{55}⋮10\)
Thật sự là cái này tách ra rất khó làm nên mình chỉ tính đơn giản thế này thôi bạn thấy dc thì tốt không dc hay không phù hợp cứ nói mình nhé mình ko giận đâu
Ta có và
và 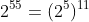
Ta có
Xét chữ số tận cùng của 2 số này đề là 2 và cấp số mũ lần lượt là 9 và 11
Nếu chỉ tính chữ số tận cùng của 2 số ta có chữ số cuối cùng của 5129 là 2 (vì 29=512:chữ số cuối)
và của 32^11 là 8(vì 211=2048:chữ số cuối)
Nếu lấy 5129+3211 ta có kết quả có chữ số tận cùng là 2+8=10
Vậy 5129+329 chia hết cho 10 hay 281+255 chia hết cho 10