Question

[Võ Đông Anh Tuấn]

Cho đường tròn ( O,R ) và đường kính MN cố định.Qua điểm M,N lần lượt kẻ 2 tiếp tuyến d 1 và d2 với đường tròn ( O,R ).Một đường thẳng đi d đi qua O cắt d1 tai E cắt d2 tại F ( E khác M ,F khác N)

a ) C/M ME = NF.

b ) TỪ O kẻ một tia vuông góc với EF cắt d2 tại K .Chứng minh tam giác EFK cân .

c ) Kẻ OI vuông góc với EK tại I.CM OI =R và EK là tiếp tuyến của đường (O,R )

d ) CMR.EM và KN ko đổi khi d quay quanh điểm O.

Answer 1

[Nguyễn Hữu Chiến]

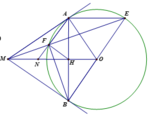
Bạn tự vẽ hình nha!!!

a) Xét\(\Delta OME\) và \(\Delta ONF\) có:

\(\widehat{OME}=\widehat{ONF}=90^o\) (d1 và d2 là tiếp tuyến của (O;R))

OM=ON( cùng =R )

\(\widehat{MOE}=\widehat{NOF}\) (2 góc đối đỉnh)

=> \(\Delta OME=\Delta ONF\) (cạnh huyền-góc nhọn)

=> ME=NF( 2 cạnh tương ứng )

b) Vì \(\Delta OME=\Delta ONF\) (c/m trên) => OE=OF (2 cạnh tương ứng)

Xét \(\Delta EFK\) có: OK là trung tuyến ứng vs EF (OE=OF)

đồng thời OK là đg cao ứng vs EF(gt)

=> \(\Delta EFK\) cân tại K (Nếu một tam giác có đg trung tuyến ứng vs 1 cạnh đồng thời là đg cao ứng vs cạnh ấy thì tam giác đó là tam giác cân)

c) Vì \(\Delta EFK\) cân tại K (c/m trên) => \(\widehat{KEF}=\widehat{KFE}\)

Hay \(\widehat{IEO}=\widehat{NFO}\)

Xét \(\Delta OEI\) và \(\Delta OFN\) có:

\(\widehat{OIE}=\widehat{ONF}=90^o\) (\(OI\perp EK \) tại I; d2 là tiếp tuyến của (O;R))

OE=OF (c/m trên)

\(\widehat{IEO}=\widehat{NFO}\) (c/m trên)

=> \(\Delta OEI=\Delta OFN\) (cạnh huyền-góc nhọn)

=> OI=ON (2 cạnh tương ứng) => OI=R (vì ON=R)

Xét đg tròn (O;OI) có: \(OI\perp EK\) tại I (gt)

=> EK là tiếp tuyến của đg tròn (O;R)

d) Hình như đề bạn sai thì phải. Theo mk nghĩ phải là chứng minh tích EM.KN ko đổi ms đúng bạn à... Nếu mk đúng thì ok! :)

Xét đg tròn (O), tiếp tuyến ME,EI,IK,KN có:

ME cắt EI tại E => OE là phân giác của \(\widehat{MOI}\) => \(\widehat{MOE}=\widehat{IOE}\) (1)

IK cắt KN tại K => OK là phân giác của \(\widehat{NOI}\) => \(\widehat{IOK}=\widehat{NOK}\) (2)

Xét \(\Delta MOE\) vuông tại M( d1 là tiếp tuyến của (O;R)) có: \(\widehat{MOE}+\widehat{MEO}=90^o\) (3)

Mặt khác \(\widehat{IOE}+\widehat{IOK}=\widehat{EOK}=90^o\) (4)

Từ (1),(2),(3) và (4) => \(\widehat{MEO}=\widehat{NOK}\)

Xét \(\Delta OME\) và \(\Delta KNO\) có:

\(\widehat{OME}=\widehat{KNO}=90^o\) (d1 và d2 là tiếp tuyến của (O;R))

\(\widehat{MEO}=\widehat{NOK}\) (c/m trên)

=> \(\Delta OME\) đồng dạng vs \(\Delta KNO\left(g.g\right)\)

=> \(\frac{OM}{KN}=\frac{EM}{ON}\) => EM.KN=OM.ON

Mà OM.ON ko đổi => EM.KN ko đổi khi d quay quanh điểm O

Answer 2

[diem ngo]

Cau a,b bạn tự cm nha

c) cm tam giac IOE= tam giac NOF(g-c-g)

=> OI=ON=R=> EK la tiep tuyen

d) xet tam giac EOK vuong tai O(gt)

\(OM^2=EI\cdot IK\left(hethucluong\right)\)

\(\Leftrightarrow R^2=ME\cdot KN\)

ma R khong doi => ME*KN khong doi

Vay EM, KN khong doi khi d quay quanh O