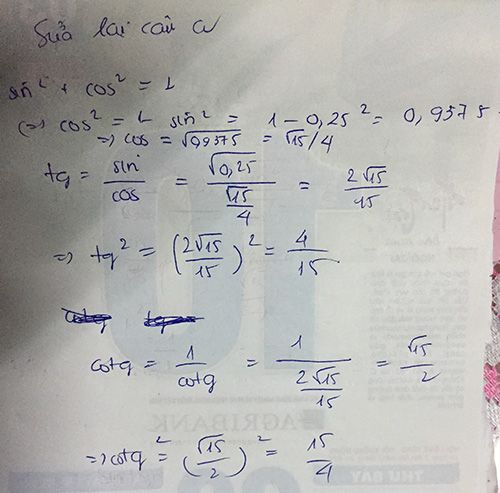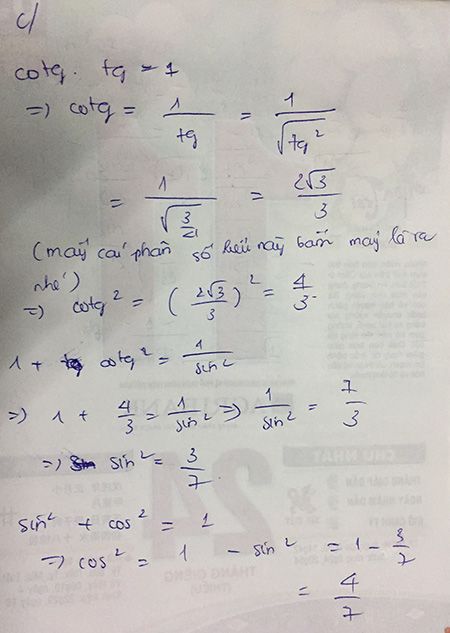Cho tg = 1/2
Tính:
cos + sin / cos - sin
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Ta có \(\tan a=3\Rightarrow\frac{\sin a}{\cos a}=3\Rightarrow\sin a=3\cos a\)
Vậy \(\frac{\cos a+\sin a}{\cos a-\sin a}=\frac{\cos a+3\cos a}{\cos a-3\cos a}=\frac{4\cos a}{-2\cos a}=-2\)
2.Ta có \(\sin^2a+\cos^2a=1\Rightarrow\cos^2a=1-\sin^2a=1-\frac{4}{9}=\frac{5}{9}\)
\(\Rightarrow\orbr{\begin{cases}\cos a=\frac{\sqrt{5}}{3}\\\cos a=\frac{-\sqrt{5}}{3}\end{cases}}\)
Với \(\cos a=\frac{\sqrt{5}}{3}\Rightarrow\tan a=\frac{\frac{2}{3}}{\frac{\sqrt{5}}{3}}=\frac{2\sqrt{5}}{5}\Rightarrow\cot a=\frac{1}{\tan a}=\frac{\sqrt{5}}{2}\)
Với \(\cos a=\frac{-\sqrt{5}}{2}\Rightarrow\tan a=\frac{-2\sqrt{5}}{5}\Rightarrow\cot a=-\frac{\sqrt{5}}{2}\)
3.
Theo hệ thức lượng trong tam giác vuông ta có \(AB^2=BH.BC\Leftrightarrow10^2=5.BC\Rightarrow BC=20\left(cm\right)\)
Theo định lí Pitago thì \(AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-10^2}=10\sqrt{3}\left(cm\right)\)
Ta có \(\tan B=\frac{AC}{AB}=\frac{10\sqrt{3}}{10}=\sqrt{3};\tan C=\frac{AB}{AC}=\frac{1}{\sqrt{3}}\)
Vậy \(\tan B=3\tan C\)

a) Cần chứng minh \(\dfrac{1-cos\alpha}{sin\alpha}=\dfrac{sin\alpha}{1+cos\alpha}\)
\(\Rightarrow sin^2\alpha=\left(1-cos\alpha\right)\left(1+cos\alpha\right)\Rightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Rightarrow sin^2\alpha+cos^2\alpha=1\)
Giả sử tam giác ABC vuông tại A
Ta có: \(\left\{{}\begin{matrix}sin^2B=\dfrac{AC^2}{BC^2}\\cos^2B=\dfrac{AB^2}{BC^2}\end{matrix}\right.\Rightarrow sin^2B+cos^2B=\dfrac{AC^2+AB^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\)
a)\(\dfrac{1-cosa}{sina}=\dfrac{sina}{1+cosa}\)
<=>\(\left(1-cosa\right)\left(1+cosa\right)=sin^2a\)
<=>\(1-cos^2a=sin^2a\) (lđ)
b)Ta có VT=\(\dfrac{cosa}{1+sina}+tga=\dfrac{cosa}{1+sina}+\dfrac{sina}{cosa}=\dfrac{cos^2a+sin^2a+sina}{\left(1+sina\right)cosa}=\dfrac{1+sina}{\left(1+sina\right)cosa}=\dfrac{1}{cosa}=vp\left(dpcm\right)\)

bài 1 : ta có : \(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-sin^2x=1-\left(0,6\right)^2=\dfrac{16}{25}\)
\(\Rightarrow cosa=\pm\dfrac{4}{5}\)
\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\pm\dfrac{3}{4}\) \(\Rightarrow cotx=\dfrac{1}{tanx}=\pm\dfrac{4}{3}\)
bài 2)
ý 1 : a) ta có : \(\dfrac{1}{cos^2a}=\dfrac{sin^2a+cos^2a}{cos^2a}=tan^2a+1\left(đpcm\right)\)
b) ta có : \(\dfrac{1}{sin^2a}=\dfrac{sin^2a+cos^2a}{sin^2a}=1+cot^2a\left(đpcm\right)\)
c) \(cos^4a-sin^4a=\left(sin^2a+cos^2a\right)\left(cos^2a-sin^2a\right)\)
\(=cos^2a-sin^2a=2cos^2a-cos^2a-sin^2a=2cos^2a-1\left(đpcm\right)\)
ý 2 :
ta có : \(tana=2\Rightarrow cota=\dfrac{1}{2}\)
ta có : \(tan^2a+1=\dfrac{1}{cos^2a}\Leftrightarrow cos^2a=\dfrac{1}{tan^2a+1}=\dfrac{1}{5}\)
\(\Rightarrow cosa=\pm\dfrac{1}{\sqrt{5}}\Rightarrow sin^2a=1-cos^2a=\dfrac{4}{5}\) \(\Rightarrow sina=\pm\dfrac{2}{\sqrt{5}}\)
vậy ............................................................................
bài 3 bạn tự luyện tập như bài 2 cho quen nha :)

đáp án :
a) \(cos^2\alpha\)
b) 1
c) \(sin^2\alpha\)
d) \(sin^2\alpha\)
e) 2
g) 1
h) \(sin^3\alpha\)
i) \(sin^2\alpha\)

\(\dfrac{\left(sina+cosa\right)^2-\left(sina-cosa\right)^2}{sina.cosa}=4\\ VT=\dfrac{sin^2a+2sinacosa+cos^2a-sin^2a+2sinacosa-cos^2a}{sinacosa}\\ =\dfrac{4sinacosa}{sinacosa}=4=VP\)
a: \(S=cos^2a\left(1+tan^2a\right)=cos^2a\cdot\dfrac{1}{cos^2a}=1\)
b: \(VP=\dfrac{1+sin2a-1+sin2a}{\dfrac{1}{2}\cdot sin2a}=\dfrac{2\cdot sin2a}{\dfrac{1}{2}\cdot sin2a}=4=VT\)