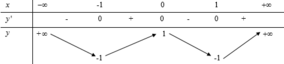
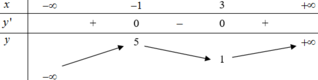
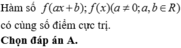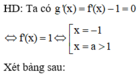Cho f(x) là hàm số bậc 4 có bảng biến thiên như sau. Hàm số Y=f(-x^2+2x)+2021/f(-x^2+2x) có bao nhiêu cực trị
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


g ' ( x ) = f ' ( x ) - 1 ; g ' ( x ) = 0 ⇔ f ' ( x ) = 1
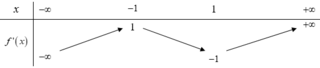
Dựa vào bảng biến thiên của hàm số y = f ' ( x ) ta có
f ' ( x ) = 1 ⇔ [ x = - 1 x = x 0 > 1
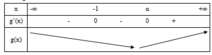
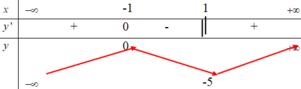
Bảng xét dấu g ' ( x )

Vậy hàm số g(x)=f(x)-x có một điểm cực trị.
Chọn đáp án D.

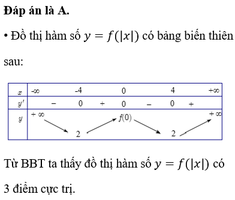
Chọn đáp án A
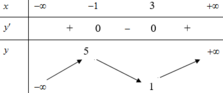
Cách vẽ đồ thị hàm số y=|f(x)|: Giữ lại phần đồ thị hàm số y=f(x) ở phía trên trục Ox và lấy đối xứng phần đồ thị của hàm số y=f(x) ở phía dưới trục Ox lên phía trên trục Ox.
Từ đó ta vẽ được đồ thị hàm số y=f(x) như sau
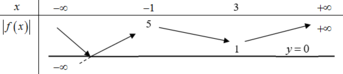
Như vậy đồ thị hàm số y=|f(x)| có 3 điểm cực trị

Chọn B.
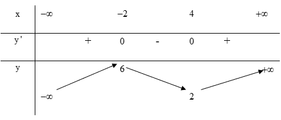
Số điểm cực trị của đồ thị hàm số y=|f(x)| bằng số điểm cực trị của đồ thị hàm số y=f(x) cộng với số giao điểm của đồ thị hàm số y=f(x) với trục hoành (không tính điểm cực trị)
Vì đồ thị hàm số y=f(x) có 2 điểm cực trị và cắt trục Ox tại 1 điểm trên đồ thị hàm số y=|f(x)| có 2 + 1 = 3 điểm cực trị