cho tam giac ABC goc A = 90 do M la trung diem cua BC. CMR AM=1/2 BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 3 2022
a: Xét tứ giác ANCB có
M là trung điểm của AC
M là trung điểm của BN
Do đó; ANCB là hình bình hành
Suy ra: CN//AB và CN=AB
=>CN⊥AC
b: Ta có: ANCB là hình bình hành
nên AN=BC và AN//BC
VM
29 tháng 11 2019
Bài 6:
b) Theo câu a) ta có \(\Delta ABD=\Delta HBD.\)
=> \(\widehat{ADB}=\widehat{HDB}\) (2 góc tương ứng).
Ta có: \(\widehat{ADB}+\widehat{HDB}=\widehat{ADH}\left(gt\right)\)
=> \(\widehat{ADB}+\widehat{HDB}=120^0\)
Mà \(\widehat{ADB}=\widehat{HDB}\left(cmt\right)\)
=> \(2.\widehat{ADB}=120^0\)
=> \(\widehat{ADB}=120^0:2\)
=> \(\widehat{ADB}=60^0.\)
=> \(\widehat{ADB}=\widehat{HBD}=60^0\)
Xét \(\Delta ABD\) có:
(định lí tổng ba góc trong một tam giác).
=> \(90^0+\widehat{ABD}+60^0=180^0\)
=> \(150^0+\widehat{ABD}=180^0\)
=> \(\widehat{ABD}=180^0-150^0\)
=> \(\widehat{ABD}=30^0\)
Vậy \(\widehat{ABD}=30^0.\)
Chúc bạn học tốt!
VM
5 tháng 10 2019
Bài 2:
a) Xét 2 \(\Delta\) \(ABM\) và \(CNM\) có:
\(AM=CM\) (vì M là trung điểm của \(AC\))
\(\widehat{AMB}=\widehat{CMN}\) (vì 2 góc đối đỉnh)
\(BM=NM\) (vì M là trung điểm của \(BN\))
=> \(\Delta ABM=\Delta CNM\left(c-g-c\right).\)
=> \(AB=CN\) (2 cạnh tương ứng)
=> \(\widehat{BAM}=\widehat{NCM}\) (2 góc tương ứng)
Ta có: \(\widehat{BAM}+\widehat{NCM}=180^0\) (vì 2 góc kề bù)
Mà \(\widehat{BAM}=90^0\left(gt\right)\)
=> \(90^0+\widehat{NCM}=180^0\)
=> \(\widehat{NCM}=180^0-90^0\)
=> \(\widehat{NCM}=90^0.\)
=> \(\widehat{BAM}=\widehat{NCM}=90^0\)
=> \(CN\perp AB.\)
b) Xét 2 \(\Delta\) \(AMN\) và \(CMB\) có:
\(AM=CM\) (như ở trên)
\(\widehat{AMN}=\widehat{CMB}\) (vì 2 góc đối đỉnh)
\(MN=MB\) (như ở trên)
=> \(\Delta AMN=\Delta CMB\left(c-g-c\right)\)
=> \(AN=BC\) (2 cạnh tương ứng)
=> \(\widehat{ANM}=\widehat{CBM}\) (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong.
=> \(AN\) // \(BC.\)
Chúc bạn học tốt!
VM
23 tháng 9 2019
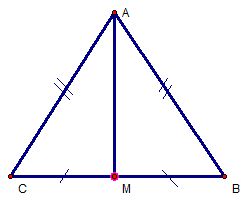
a) Xét 2 \(\Delta\) \(ABM\) và \(ACM\) có:
\(AB=AC\left(gt\right)\)
\(BM=CM\) (vì M là trung điểm của \(BC\))
Cạnh AM chung
=> \(\Delta ABM=\Delta ACM\left(c-c-c\right)\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng)
=> \(AM\) là đường phân giác của \(\widehat{A}.\)
b) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
Có \(AM\) là đường phân giác (cmt) đồng thời \(AM\) cũng là đường cao của \(\Delta ABC.\)
=> \(AM\) là đường cao của \(\Delta ABC.\)
c) Theo câu b) ta có \(\Delta ABC\) cân tại A.
Có \(AM\) là đường cao đồng thời \(AM\) cũng là đường trung trực của \(\Delta ABC.\)
=> \(AM\) là đường trung trực của \(BC.\)
Chúc bạn học tốt!
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến ứng với cạnh huyền BC
nên AM=1/2BC(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)