cách biện luận giải hệ phương trình 2 ẩn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 5 2020
\(m^2x=m\cdot\left(x+2\right)-2\)
\(\Leftrightarrow x\left(m^2-m\right)-2m+2=0\)
*Nếu m=1 <=> m^2 - m = 0 \(\Leftrightarrow-2.1+2=0\left(Đ\right)\)
=> Với m =1 thì pt thỏa mãn với mọi x thuộc R
*Nếu \(m\ne1\Leftrightarrow x=\frac{2m-2}{m^2-m}\)
=> Với \(m\ne1\text{ thì }x=\frac{2m-2}{m^2-m}\)
Vậy ....
SN
4
10 tháng 2 2018
\(mx^2-2=4x+m\)
\(\Leftrightarrow mx^2-4x=m+2\)
\(\Leftrightarrow x.\left(mx-4\right)=m+2\)
nếu \(mx-4\ne0\Leftrightarrow m\ne\frac{4}{x}\)\(\Leftrightarrow x\ne\pm1\) thì phương trình trên có 1 nghiệm duy nhất
\(x=\frac{m+2}{mx-4}\)
vậy khi \(m\ne\frac{4}{x}\) thì phương trình đã cho có nghiệm duy nhất \(x=\frac{m+2}{mx-4}\)
+) nếu \(m=\frac{4}{x}\) thì phương trình có dạng \(0x=m+2\) ( pt này có vô số nghiệm )
vậy khi \(m=\frac{4}{x}\)thì pt đã cho có vô số nghiệm
nghiệm tổng quát của phương trình là \(x\in R\)
10 tháng 2 2018
Tham khảo bài này :
4 bài toán này đều là dạng bài Giải và biện luận PT bậc nhất
Nên cách giải cũng đơn giản thôi, bạn chỉ cần chuyển các PT trên về dạng ax+b=0 là được. Mình sẽ làm thử cho bạn xem nha?
1> PT<=> (m^2+1)x -2m+3=0
Dễ thấy : a=m^2+1# 0 ( với mọi giá trị của m )
Do đó : PT luôn có nghiệm duy nhất x=(2m-3)/(m^2+1)
2> PT có dạng : -m^2 - 3m = -2m + 6
<=> -m^2 - m -6 =0
vô nghiệm với mọi giá trị của m
=> PT đã cho luôn vô nghiệm với mọi giá trị của m
3> PT <=> (m-1)x -m^2-m+2 = 0
TH1 : m-1# 0 <=> m # 1
thì PT luôn có nghiệm duy nhất : x=(m^2+m-2)/(m-1) = m+2
TH2 : m-1=0 <=> m = 1
thì PT có dạng : 0x+0 = 0
=> PT có vô số nghiệm ( hay PT có nghiệm x tùy ý )
Kết luận :
Với m # 1 : PT có nghiệm duy nhất x = m+2
Với m=1 : PT có vô số nghiệm
4> (m^2-3m+2)x -m^2+m = 0
TH1 : m^2-3m+2 = 0 <=> m=1 hoặc m=2
- Nếu m=1 thì PT có dạng : 0x+0=0
=> PT có vô số nghiệm
- Nếu m=2 thì PT có dạng : 0x-2=0
=> PT vô nghiệm
TH2 : m^2-3m+2 # <=> m # 1 và m # 2
thì PT có nghiệm duy nhất x=(m^2-m)/(m^2-3m+2) = m/(m-2)
Kết luận :
Với m=1 : PT có vô số nghiệm
Với m=2 :PT vô nghiệm
Với m # 1 và m # 2 thì PT có nghiệm duy nhất x=m/(m-2)
T
31 tháng 12 2018
\(\hept{\begin{cases}mx+y=1\left(1\right)\\3x-\left(m+1\right)y=-3\left(2\right)\end{cases}}\).
Từ phương trình (1) suy ra \(y=1-mx\)
Thay vào phương trình (2),ta có: \(3x-\left(m+1\right)\left(1-mx\right)=-3\)
\(\Leftrightarrow\left(m+1\right)\left(1-mx\right)=3x+3\)
\(\Leftrightarrow-m^3x-mx+m=3x+2\)
\(\Leftrightarrow-m\left(m^2x+x-1\right)-3x=2\)
Với m = 0 phương trình có nghiệm duy nhất: \(x=-\frac{2}{3}\)
Xét tiếp tục với \(m\ne0\) nhé bạn.
T
31 tháng 12 2018
Thôi chết giải nhầm.
Giải
Từ phương trình thứ nhất của hệ suy ra \(y=1-mx\)
Thay vào phương trình thức hai của hệ được: \(3x-\left(m+1\right)\left(1-mx\right)=-3\)
\(\Leftrightarrow\left(m+1\right)\left(1-mx\right)=3x+3\)
\(\Leftrightarrow m\left(1-mx\right)+1\left(1-mx\right)=3x+3\)
\(\Leftrightarrow-m^2x-mx+m=3x+2\)
Với m = 0 thì \(PT\Leftrightarrow3x+2=0\Leftrightarrow x=-\frac{2}{3}\)
Với \(m\ne0\) .....giải tiếp ....
^^
VH
0
TA
1 tháng 2 2021
• PT có nghiệm duy nhất \( \Leftrightarrow \dfrac{1}{m} \ne \dfrac{-2}{1} \Leftrightarrow m \ne \dfrac{-1}{2}\)
• PT vô nghiệm \(\Leftrightarrow \dfrac{1}{m} =\dfrac{-2}{1} \ne \dfrac{1}{2} \Leftrightarrow m=\dfrac{-1}{2}\)
• PT có vô số nghiệm \(\Leftrightarrow \dfrac{1}{m} = \dfrac{-2}{1} = \dfrac{1}{2} (\text{Vô lý})\)
Vậy....
9 tháng 1 2023
2mx+y=2 và 8x+my=m+2
=>y=2-2mx và 8x+m(2-2mx)=m+2
=>\(\left\{{}\begin{matrix}8x+2m-2m^2x-m-2=0\\y=-2mx+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(-2m^2+8\right)=-m+2\\y=-2mx+2\end{matrix}\right.\)
=>2(m-2)(m+2)x=m-2 và y=-2mx+2
Nếu m=2 thì hệpt có vô số nghiệm
Nếu m=-2 thìhệ pt vn
Nếu m<>2; m<>-2 thì hệ phương trình có nghiệm duy nhất là:
\(\left\{{}\begin{matrix}x=\dfrac{1}{2\left(m+2\right)}\\y=-2m\cdot\dfrac{1}{2\left(m+2\right)}+2=-\dfrac{m}{m+2}+2=\dfrac{-m+2m+4}{m+2}=\dfrac{m+4}{m+2}\end{matrix}\right.\)
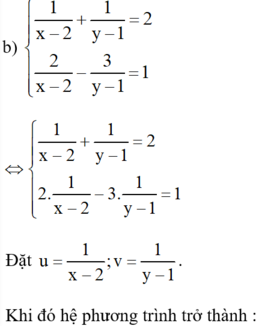
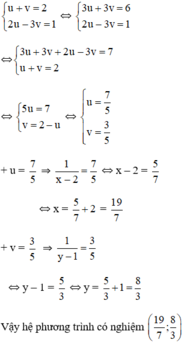
Bạn sử dụng Định thức để biện luận nhé :)