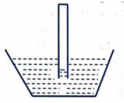
Người ta dựng 1 ống thuỷ tinh vuông góc với mặt thoáng nước trong bình, hai ổng đều hở, phần ống nhô lên mặt nước có chiều cao là 5 cm, sau đó rót dầu vào ống phải có chiều cao là bao nhiêu để nó hoàn toàn chứa dầu? Cho trọng lượng riêng của nước là 10000N/ m 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều cao của phần ống thủy tinh nhô lên mặt nước là \(h_1\), phần nhúng trong nước là \(h_2\)
Điểm A, B nằm trong 1 mp
Ta có : \(P_A=P_B\)
\(P_A=P_{kq}+d_1h_2\)
\(P_B=P_{kq}+d_2\left(h_1+h_2\right)\)
\(\rightarrow d_1h_2=d_2\left(h_1+h_2\right)\)
\(\rightarrow\left(d_1-d_2\right)h_2=d_2.h_1\)
\(\rightarrow h_2=\dfrac{8000.7}{10000-8000}28\left(cm\right)\)
Chiều cao ống :
\(h=h_1+h_2=35\left(cm\right)\)

khoảng cách từ đáy ống đến mặt thoáng là :
h1=h-10=60-10=50(cm)=0,5(m)
áp suát tác dụng lên đáy ống là :
P=h1.d=0,5.10000=5000(N/m2)
khpảng cách từ điểm đó đén mặt thoáng là : h2=30-10=20(cm)=0,2(m)
áp suất tác dụng lên điểm đó là : P2=d.h2=10000.0,2=2000(N/m2)

Gọi A là điểm nằm trên mặt thoáng của chất lỏng ở trong ống, B là điểm nằm ngoài ống nhưng có cùng độ cao với A. Khi mực nước ở trong vòng vòng ngoài ống cân bằng nhau, ta có:
p A = p B ⇒ p = p 0 + d.h = 1 , 013 . 10 5 + 1000.0,4 = 101700(Pa)
Vì nhiệt độ là không đổi, do đó áp dụng định luật Bôi-lơ-Ma-ri-ốt cho khối khí trong ống trước và sau khi nhúng, ta có:
p 0 . V 0 = p . V ⇔ V V 0 = l l 0 = p 0 p
Trong đó l và l0 là chiều cao cột không khí trước và sau khi nhúng
l = l 0 P 0 P = l . 101300 101700 = 0 , 996 m = 99 , 6 c m
Chiều cao cột nước trong ống là: H = l 0 – l = 100 - 99 , 6 = 0 , 4 ( c m )

a, thể tích của dầu là : Vd = \(\dfrac{m_d}{D_d}\) = \(\dfrac{0,04}{800}\) = 5.10-5 (m3)
chiều cao của cột dầu là : hd = \(\dfrac{V_d}{S}\) = \(\dfrac{5.10^{-5}}{0,0002}\) = 0,25 (m)
xét điểm A nằm trên cùng mặt phân cách giữa nước và dầu và điểm B nằm trên cùng mặt phân cách ở ngoài ống thủy tinh
ta có : PA = PB
<=> dd . hd = dnước . h2 ( h2 là độ cao mực dầu trong chậu nước )
<=> 8000.0,25 = 10000. h2
<=> h2 = 0,2 m
=> h = hd - h2 = 0,25 - 0,2 = 0,05 m
độ chênh lệch hai mặt thoáng là 0,05m
b, xét điểm A nằm trên mặt phân cách gữa nước và dầu và điểm B cùng mặt phân cách ở ngoài ống
PA = PB
=> dd . h = dnước . h3
=> 8000.0,5 = 10000. h3
=> h3 = 0,4 m
vậy phải đặt ống cách mặt thoáng 0,4m để có thể rót dầu vào đầy ống
=> miệng ống cách mặt nước 0,5-0,4=0,1m
c, khi kéo ống lên 1 đoạn 2cm = 0,002m, một phần dầu bị chảy ra ngoài và khi đã ổn định chiều cao cột dầu còn lại trong ống là l1 , ta có :
Pc = dd.l1 = dnước.( l - y-2 )
=> l1 = \(\dfrac{d_{nước}}{d_d}\) . ( 0,4-0,002) = \(\dfrac{10000}{8000}\) . 0,38 = 0,475 (m)
tương tự với kéo lên một đoạn là x , ta có :
=> l1 = \(\dfrac{d_{nước}}{d_d}\) . ( 0,4 - x ) = \(\dfrac{10000}{8000}\) . (0,4-x)
vậy ....