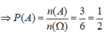Gieo 1 con súc sắc 6 lần độc lập. tính xác xuất để không lần nào xuất hiện mặt có số chấm là 1 số chẵn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2021
Xác suất:
a. \(\dfrac{3}{6}.\dfrac{3}{6}=\dfrac{1}{4}\)
b. \(\dfrac{6}{36}=\dfrac{1}{6}\)
c. Xác suất mặt 6 chấm ko xuất hiện lần nào: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất mặt 6 xuất hiện ít nhất 1 lần: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
d. Các trường hợp tổng 2 mặt lớn hơn hoặc bằng 10: (6;4), (4;6); (5;5); (5;6);(6;5);(6;6) có 6 khả năng
\(\Rightarrow36-6=30\) khả năng tổng số chấm bé hơn 10
Xác suất: \(\dfrac{30}{36}=\dfrac{5}{6}\)
CM
17 tháng 4 2018
Đáp án A
Tổng số chấm trên mặt xuất hiện trong hai lần gieo ≥ 11 khi các kết quả là 6 ; 6 , 5 ; 6 , 6 ; 5
Gọi x là xác suất xuất hiện mặt 6 chấm suy ra x 2 là xác suất xuất hiện các mặt còn lại
Ta có 5. x 2 + x = 1 ⇒ x = 2 7 .
Do đó xác suất cần tìm là 2 7 2 + 2 7 . 1 7 + 1 7 . 2 7 = 8 49
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2020
a. Có 3 mặt nguyên tố: 2,3,5 nên xác suất xuất hiện số nguyên tố ở mỗi lần gieo là \(\dfrac{3}{6}=\dfrac{1}{2}\)
Xác suất 2 lần đều xuất hiện số nguyên tố: \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)
b. Xác suất để lần 1 xuất hiện mặt 6 chấm: \(\dfrac{1}{6}\)
c. Xác suất ít nhất 1 lần xuất hiện mặt 6 chấm: \(\dfrac{2.6-1}{36}=\dfrac{11}{36}\)
d. Xác suất ko lần nào xuất hiện 6 chấm: \(1-\dfrac{11}{36}=\dfrac{25}{36}\)
CM
2 tháng 12 2019
Đáp án A.
Tổng số chấm xuất hiện trong hai lần gieo lớn hơn hoặc bằng 11 khi các kết quả là (6;6), (5;6), (6;5)
Gọi x là xác suất xuất hiện mặt 6 chấm suy ra x 2 là xác suất xuất hiện các mặt còn lại.
Ta có: 5 x 2 + x = 1 ⇒ x = - 2 7
Do đó xác suất cần tìm là: 2 7 2 + 2 7 . 1 7 + 1 7 . 2 7 = 8 49 .
CM
11 tháng 1 2019
a) Ω = {S1, S2, S3, S4, S5, N1, N2, N3, N4, N5}
b)
A = {S2, S4, S6};
B = {N1, N3, N5}.
CM
29 tháng 5 2019
Đáp án là A.
• Số phần tử không gian mẫu n ( Ω ) = 36
• Gọi biến cố A: " Số chấm xuất hiện trên mặt của hai con súc sắc là số chẳn".
Ta có các khả năng xảy ra:
CM
13 tháng 5 2018
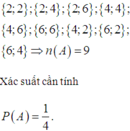
Đáp án là A
Số phần tử không gian mẫu n Ω = 36
Gọi biến cố " Số chấm xuất hiện trên mặt của hai con súc sắc là số chẳn".
Ta có các khả năng xảy ra:
2 ; 2 ; 2 ; 4 ; 2 ; 6 ; 4 ; 4 ; 4 ; 6 ; 6 ; 6 ; 4 ; 2 ; 6 ; 2 ; 6 ; 4 ⇒ n A = 9
Xác suất cần tính: P A = 1 4