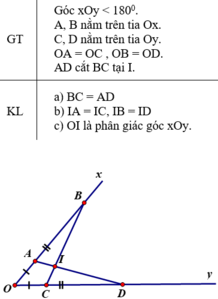
1) Cho góc xOy khác góc bẹt. Trên tia Ox lấy 2 điểm A và B, trên tia đối Oy lấy 2 điểm C và D sao cho OA = OC, OB = OD. Gọi I là giao điểm của 2 đoạn thẳng AD và BC. CMR:
a) BC = AD
2)Cho tam giác ABC có AB = AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho AM = MD
a) CMR tam giác ABM = tam giác DCM
b) CMR AB//CD
c) CMR AM vuông góc với BC
Nhớ vẽ hình và viết giả thiết và kết luận nha
Giúp mình với![]() Mình cần gấp
Mình cần gấp

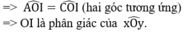


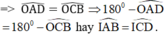
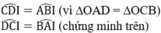
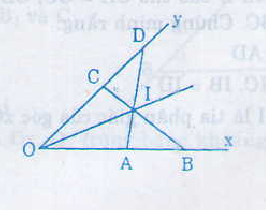
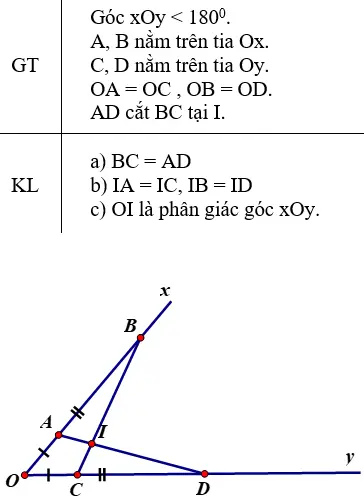
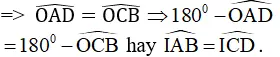
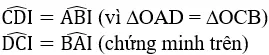
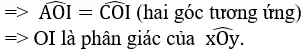
1/ Ta có hình vẽ:
Xét tam giác OAD và tam giác OBD có:
O: góc chung
OA = OC (GT)
OB = OD (GT)
=> tam giác OAD = tam giác OBD (c.g.c)
=> BC = AD (2 cạnh tương ứng)
Vậy BC = AD (đpcm)
2/ Ta có hình vẽ:
Mình quên kí hiệu AB = AC rồi, bạn tự bổ sung thêm nhé
a/ Xét tam giác ABM và tam giác DCM có:
AM = MD (GT)
BM = MC (GT)
\(\widehat{AMB}\)=\(\widehat{CMD}\) (đối đỉnh)
=> tam giác ABM = tam giác DCM (c.g.c)
b/ Ta có: tam giác ABM = tam giác DCM (câu a)
=> \(\widehat{ABM}\)=\(\widehat{MCD}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
nên AB//CD (đpcm)
c/ Xét tam giác ABM và tam giác ACM có:
AM: cạnh chung
BM = MC (GT)
AB = AC (GT)
=> tam giác ABM = tam giác ACM (c.c.c)
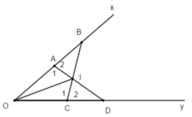
=> \(\widehat{AMB}\)=\(\widehat{AMC}\) (2 góc tương ứng)
Mà \(\widehat{AMB}\) + \(\widehat{AMC}\) = 1800 (kề bù)
=> \(\widehat{AMB}\) = \(\widehat{AMC}\) = 900
Vậy AM \(\perp\)BC (đpcm)