Cho x + y = 7 và xy = 12 thì |x - y| = ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
L
1
27 tháng 8 2016
\(xy=12=3.4\Leftrightarrow\frac{x}{y}=\frac{3}{4}\Leftrightarrow4x=3y\Leftrightarrow\frac{x}{3}=\frac{y}{4}\)
Vì các trường hợp Ư(12) khi tính ra x,y đều ra kq giống nhau nên ta chỉ lấy 1 trường hợp là 12=3*4
Áp dụng tc dãy tỉ
\(\frac{x}{3}=\frac{y}{4}=\frac{x+y}{3+4}=\frac{7}{7}=1\)
Với \(\frac{x}{3}=1\Leftrightarrow x=3\)
Với \(\frac{y}{4}=1\Leftrightarrow y=4\)
Suy ra |x-y|=|3-4|=|-1|=1
22 tháng 7 2023
`a, (x-y)^2 = (x+y)^2 - 4xy = 12^2 - 35 . 4 = 144 - 140 = 4`.
`b, (x+y)^2 = (x-y)^2 + 4xy = 8^2 + 20.4 = 64 + 80 = 144`
`c, x^3 + y^3 = (x+y)^3 - 3xy(x+y) = 5^3 - 3 . 6 . 5 = 125 - 90 = 35`
`d, x^3 - y^3 = (x-y)^3 - 3xy(x-y) = 3^3 - 3 .40 . 3 = 27 - 360 = -333`.
NV
3
ML
10 tháng 7 2015
\(x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2=\left[\left(x+y\right)^2-2xy\right]^2-2\left(xy\right)^2\)
\(=\left(7^2-2.12\right)^2-2.12^2=337\)
10 tháng 7 2015
(x + y)^2 = 7^2 = 49
x^2 + 2xy + y^2 = 49
x^2 + y^2 + 12 = 49
x^2 + y^2 = 37
( x^2 + y^2 )^2 = 37^2 = 1369
x^4 + 2x^2y^2 + y^4 = 1369
x^4 + y^4 + 2.(xy)^2 = 1369
x^4 + y^4 + 2.12^2 = 1369
x^4 + y^4 + 288 = 1369
x^4 + y^4 = 1081
VẬy A = 1081
CM
10 tháng 6 2017
Điều kiện y ≠ 0
Hệ phương trình tương đương với x + y + x y = 7 ( 1 ) x x y + 1 = 12 ( 2 )
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12
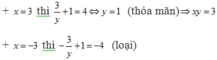
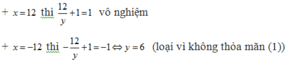
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
PT
2
13 tháng 7 2017
Đề sai rồi bạn ơi. xy=112 mới đúng nha!
\(\frac{x}{4}=\frac{y}{7}=k\Rightarrow\hept{\begin{cases}x=4k\\y=7k\end{cases}}\)
Ta có xy=112
4k.7k=112
28k2=112
k2=4
k=2, k=-2
Với k=2 thì x=8, y= 14
Với k=-2 thì x=-8, y=-14
DP
13 tháng 7 2017
\(\frac{x}{4}=\frac{y}{7}\Leftrightarrow7x=4y\Leftrightarrow x=\frac{4y}{7}\).Thay vào biểu thức x . y = 12 . Ta được :
\(\frac{4y}{7}\cdot y=12\Leftrightarrow4y^2=84\Leftrightarrow y^2=21\Leftrightarrow y=\sqrt{21};y=-\sqrt{21}\)
Với y = \(\sqrt{21}\)thì x = \(\frac{4\cdot\sqrt{21}}{7}\)
Với y = \(-\sqrt{21}\)thì x = \(-\frac{4\cdot\sqrt{21}}{7}\)
25 tháng 6 2023
Câu 3:
a: A(x)=x^3+3x^2-4x-12
B(x)=x^3-3x^2+4x+18
A(x)+B(x)
=x^3+3x^2-4x-12+x^3-3x^2+4x+18
=2x^3+6
A(x)-B(x)
=x^3+3x^2-4x-12-x^3+3x^2-4x-18
=6x^2-8x-30
b: A(-2)=(-8)+3*4-4*(-2)-12
=-20+3*4+4*2=0
=>x=-2 là nghiệm của A(x)
B(-2)=(-8)-3*(-2)^2+4*(-2)+18=-10
=>x=-2 ko là nghiệm của B(x)
NT
1
NC
25 tháng 8 2020
Bài làm:
Dễ thấy a,b,c khác 0
Ta có: \(\frac{xy}{x+y}=\frac{12}{7}\Leftrightarrow\frac{x+y}{xy}=\frac{7}{12}\Leftrightarrow\frac{1}{x}+\frac{1}{y}=\frac{7}{12}\) (1)
Tương tự ta tách ra được: \(\frac{1}{y}+\frac{1}{z}=-\frac{1}{6}\) (2) ; \(\frac{1}{z}+\frac{1}{x}=-\frac{1}{4}\) (3)
Cộng vế (1);(2) và (3) lại ta được:
\(2\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=\frac{1}{6}\Rightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{12}\) (4)
Cộng vế (1) và (2) lại ta được: \(\frac{1}{x}+\frac{2}{y}+\frac{1}{z}=\frac{5}{12}\)
Thay (4) vào ta được: \(\frac{1}{y}+\frac{1}{12}=\frac{5}{12}\Leftrightarrow\frac{1}{y}=\frac{1}{3}\Rightarrow y=3\)
Từ đó ta dễ dàng tính được: \(\hept{\begin{cases}\frac{1}{x}=\frac{7}{12}-\frac{1}{3}=\frac{1}{4}\\\frac{1}{z}=-\frac{1}{6}-\frac{1}{3}=-\frac{1}{2}\end{cases}}\Rightarrow\hept{\begin{cases}x=4\\z=-2\end{cases}}\)
Vậy \(\left(x;y;z\right)=\left(4;3;-2\right)\)
NV
1
AH
Akai Haruma
Giáo viên
30 tháng 9 2023
Lời giải:
Đặt $xy=a; x+y=b$ thì theo đề ta có:
$a+b=-1$ và $ab=-12$
Ta cần tính: $A=(x+y)^3-3xy(x+y)=b^3-3ab=b^3-3(-12)=b^3+36$
Từ $a+b=-1\Rightarrow a=-b-1$. Thay vào $ab=-12$
$\Rightarrow (-b-1)b=-12$
$\Leftrightarrow (b+1)b=12$
$\Leftrightarrow b^2+b-12=0$
$\Leftrightarrow (b-3)(b+4)=0$
$\Leftrightarrow b=3$ hoặc $b=-4$
Nếu $b=3$ thì $A=3^3+36=63$
Nếu $b=-4$ thì $A=(-4)^3+36=-28$
(x+y)2 = x2+y2+2xy = 49 <=> x2+y2-2xy+4xy=49 <=>(x-y)2=49-4xy=49-4.12=1 <=> |x-y|=1
x, y là nghiệm của phương trình t^2 - 7t +12 = 0 => t1 = 3; t2 = 4
x=3 thì y = 4; x= 4 thì y = 3=>|x-y|=1
2 tick cho mình nha