Câu2: Giải phương trình
K
Khách
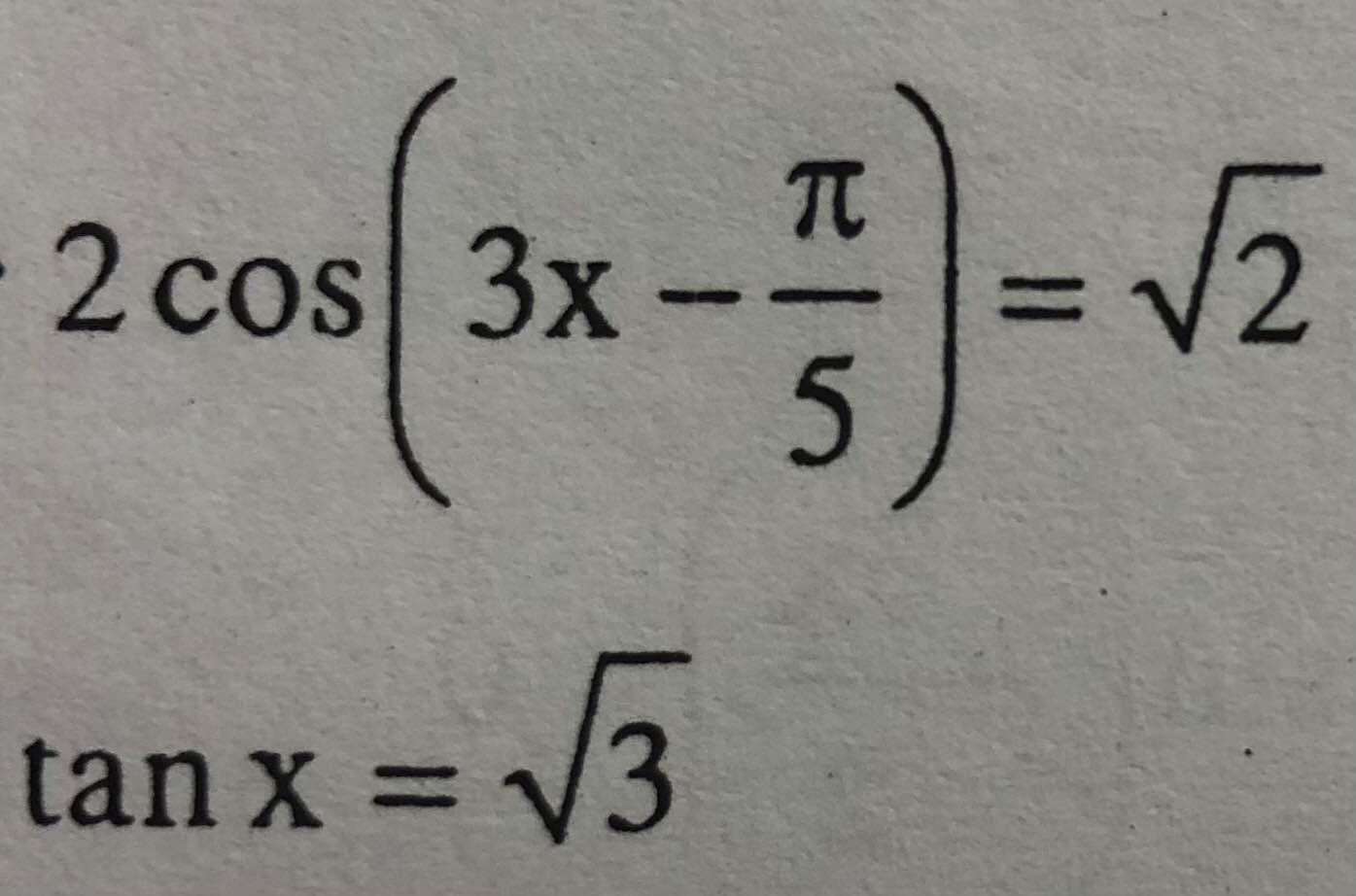
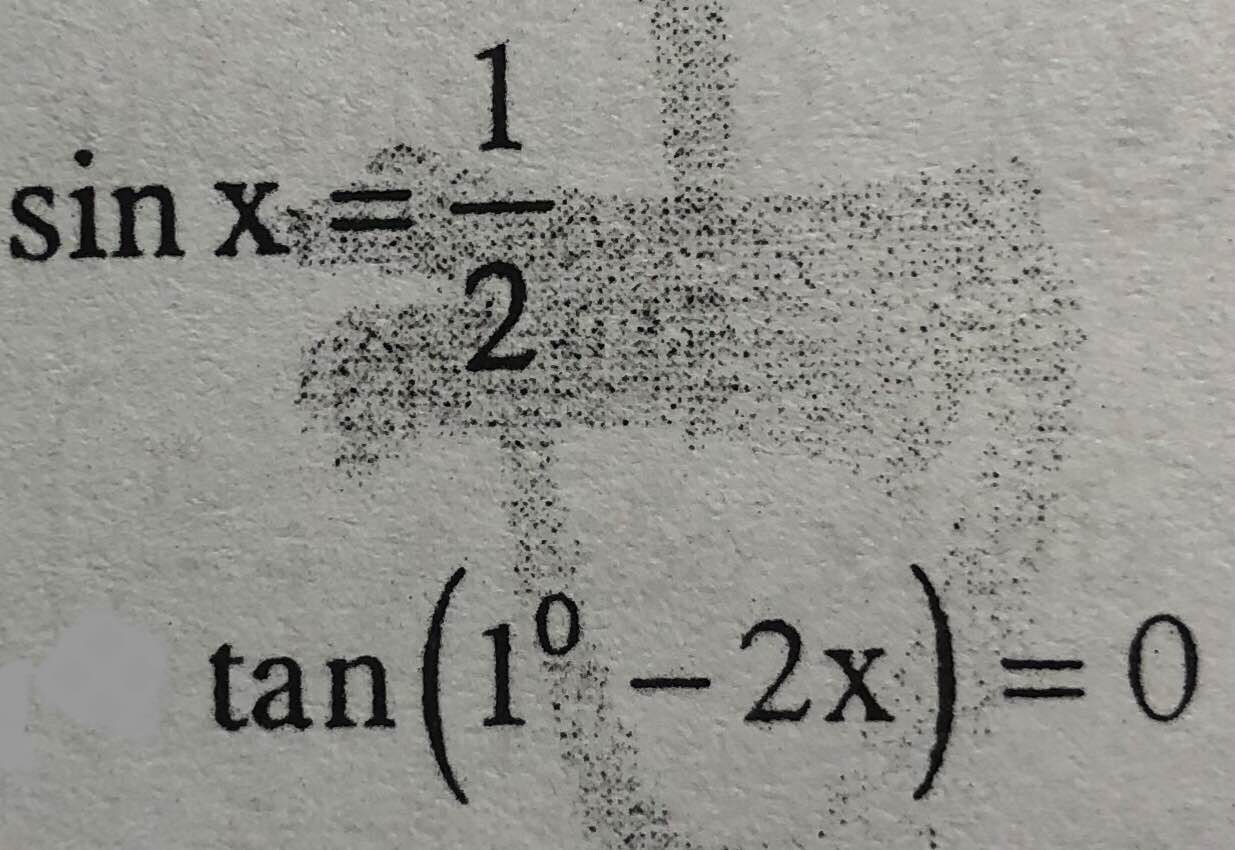
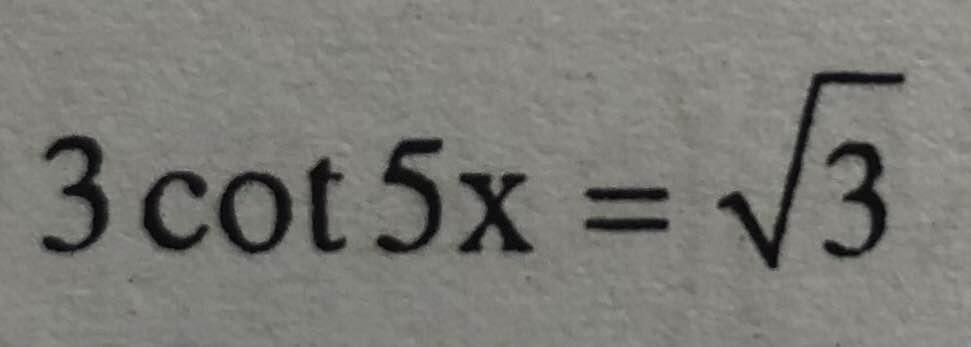
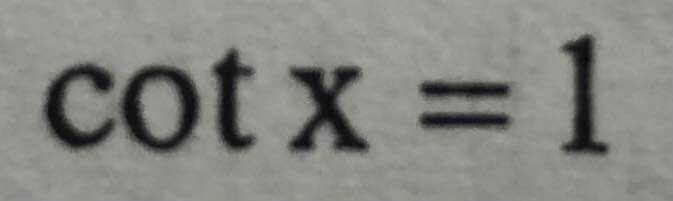
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
18 tháng 9 2021
a, \(Ba\left(NO_3\right)_2\rightarrow Ba^{2+}+2NO_3^-\)
\(HNO_3\rightarrow H^++NO_3^-\)
\(KOH\rightarrow K^++OH^-\)
b, \(HClO⇌H^++ClO^-\)
\(HNO_2⇌H^++NO_2^-\)
\(H_2CO_3⇌2H^++CO_3^{2-}\)
16 tháng 2 2017
Câu 1 : \(a,\hept{\begin{cases}4x+7y=16\left(1\right)\\4x-3y=-24\left(2\right)\end{cases}}\)
Lấy ( 1 ) trừ ( 2 ) ta được :
10y = 40
=> y = 4
Thay y = 4 vào ( 1 ) ta được :
4x + 7 x 4 = 16
=> 4x + 28 = 16
=> 4x = 16 - 28
=> 4x = - 12
=> x = - 3
Vậy x = - 3 ; y = 4
\(b,\hept{\begin{cases}3x+5y=1\\2x+y=-4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3x+5.\left(-4-2x\right)=1\\y=-4-2x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3x-20-10x=1\\y=-4-2x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-7x-20=1\\y=-4-2x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-7x=21\\y=-4-2x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=-3\\y=-4-2.\left(-3\right)\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=-3\\y=2\end{cases}}\)
14 tháng 3 2023
Câu 1:
a, \(C_2H_4+Br_2\rightarrow C_2H_4Br_2\)
\(C_2H_2+2Br_2\rightarrow C_2H_2Br_4\)
b, Ta có: \(n_{C_2H_4}+n_{C_2H_2}=\dfrac{22,4}{22,4}=1\left(mol\right)\left(1\right)\)
Theo PT: \(n_{Br_2}=n_{C_2H_4}+2n_{C_2H_2}=0,8.2=1,6\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{C_2H_4}=0,4\left(mol\right)\\n_{C_2H_2}=0,6\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{C_2H_4}=\dfrac{0,4.22,4}{22,4}.100\%=40\%\\\%V_{C_2H_2}=60\%\end{matrix}\right.\)
Câu 2:
Ta có: \(n_{CO_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)=n_C\)
\(n_{H_2O}=\dfrac{1,8}{18}=0,1\left(mol\right)\Rightarrow n_H=0,1.2=0,2\left(mol\right)\)
Gọi CTPT của A là CxHy.
⇒ x:y = 0,1:0,2 = 1:2
→ A có CTPT dạng (CH2)n
Mà: MA = 14.2 = 28 (g/mol)
\(\Rightarrow n=\dfrac{28}{12+1.2}=2\)
Vậy: CTPT của A là C2H4.
CTCT: CH2=CH2.
C
1
MH
14 tháng 12 2021
Tham khảo
Trình duyệt web là một ứng dụng phần mềm để truy cập thông tin trên World Wide Web. Mỗi trang web, hình ảnh và video riêng lẻ được xác định bằng một URL riêng biệt, cho phép các trình duyệt truy xuất và hiển thị chúng trên thiết bị của người dùng mới.
Dưới đây là một số cái tên trình duyệt web phổ biến hiện nay cùng các ưu, khuyết điểm của nó.Trình duyệt web Google Chrome. ...Cốc Cốc. ...Mozilla Firefox. ...Trình duyệt web Safari. ...Opera. ...InteExplorer.
24 tháng 3 2020
tôi bị mất ních olm
https://olm.vn/thanhvien/khoi198a2006
ai lấy lại hộ zới
C
12 tháng 3 2023
Câu 1 Hoàn thành PTHH:
\(1)2KMnO_4\underrightarrow{t^o}K_2MnO_4+MnO_2\downarrow+O_2\uparrow\\ 2)FeO+2HCl\rightarrow FeCl_2+H_2O\\ 3)Fe_2O_3+3H_2SO_4\rightarrow Fe_2\left(SO_4\right)_3+3H_2O\\ 4)4P+5O_2\underrightarrow{t^o}2P_2O_5\)
Câu 2
\(n_{Zn}=\dfrac{m}{M}=\dfrac{13}{65}=0,2\left(mol\right)\)
a) \(PTHH:Zn+H_2SO_4\rightarrow ZnSO_4+H_2\)
1 1 1 1
0,2 0,2 0,2 0,2
b) \(V_{H_2}=n.24,79=0,2.24,79=4,958\left(l\right)\)
c) \(m_{H_2SO_4}=n.M=0,2.\left(2+32+16.4\right)=19,6\left(g\right).\)
12 tháng 3 2023
câu 1
(1)2KMnO4➞(to)K2MnO4+MnO2+O2
(2)FeO+2HCl➞FeCl2+H2O
(3)Fe2O3+3H2SO4➞Fe2(SO4)3+3H2O
(4)4P+5O2➞2P2O5
Câu2
a)PTHH:Zn+H2SO4➞ZnSO4+H2
b)nZn=\(\dfrac{13}{65}\)=0,2(m)
n\(_{H_2SO_4}\)=\(\dfrac{24,5}{98}\)=0,25(m)
PTHH : Zn + H2SO4 ➞ ZnSO4 + H2
tỉ lệ :1 1 1 1
số mol
ban đầu :0,2 0,25
ta có tỉ lệ:\(\dfrac{0,2}{1}\)<\(\dfrac{0,25}{1}\)->H2SO4 dư
PTHH : Zn+ H2SO4 ➞ + ZnSO4+H2
tỉ lệ :1 1 1 1
số mol :0,2 0,2 0,2 0,2
v\(_{H_2}\)=0,2.22,4=4,48(l)
c)m\(_{ZnSO_4}\)=0,2.161=32,2(g)
m\(_{H_2}\)=0,2.2=0,4(g)
a.
\(2cos\left(3x-\dfrac{\pi}{5}\right)=\sqrt{2}\)
\(\Leftrightarrow cos\left(3x-\dfrac{\pi}{5}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{\pi}{5}=\dfrac{\pi}{4}+k2\pi\\3x-\dfrac{\pi}{5}=-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=\dfrac{9\pi}{20}+k2\pi\\3x=-\dfrac{\pi}{20}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3\pi}{20}+\dfrac{k2\pi}{3}\\x=-\dfrac{\pi}{60}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
b.
\(tanx=\sqrt{3}\)
\(\Leftrightarrow tanx=tan\left(\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
c.
\(sinx=\dfrac{1}{2}\)
\(\Leftrightarrow sinx=sin\left(\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)