làm sao để giải bài toán phương trinh bậc hai ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 5 2016
Gọi số bé là x (x>0)
Vậy số lớn là 3x
Hiệu 2 số là 50 nên ta có phương trình:
3x-x=50
2x=50
x=25 (tmđk)
Vậy số bé là 25 và số lớn là 75
15 tháng 5 2016
Gọi số bé là x (x>0)
Vậy số lớn là 3x
Hiệu 2 số là 50 nên ta có phương trình:
3x-x=50
2x=50
x=25 (tmđk)
Vậy số bé là 25 và số lớn là 75
D
1
ML
13 tháng 3 2021
Bài 1:
Thuật toán:
B1: Nhập a,b,c
B2: Tính \(\Delta\) = b2-4ac;
B3: Kiểm tra nếu \(\Delta\) >0 phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}\text{ }}{2a}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\)
B4: Kiểm tra nếu \(\Delta\)<0 thì phương trình vô nghiệm
B5: Kiểm tra nếu \(\Delta\)=0 phương trình có 2 nghiệm kép \(x_1=x_2=-\dfrac{b}{2a}\)
Viết chương trình:
Program HOC24;
var a,b,c: integer;
x1,x2: real;
denta: longint;
begin
write('Nhap a; b; c: '); readln(a,b,c);
denta:=b*b-4*a*c;
if denta>0 then
begin
write('x1= ',(-b+sqrt(denta))/(2*a):1:2);
write('x2= ',(-b-sqrt(denta))/(2*a):1:2);
end;
if denta<0 then write('Phuong trinh vo nghiem');
if denta=0 then write('x= ',-b/2*a:1:2);
readln
end.
ML
13 tháng 3 2021
Bài 2:
Thuật toán:
B1: Nhập a,b
B2: Kiểm tra nếu a=0 và b=0 thì phương trình có vô số nghiệm
B3: Kiểm tra nếu a=0 thì phương trình vô nghiệm
B4: Kiểm tra nếu a khác 0 thì có nghiệm x=-b/a;
Viết chương trình:
Program HOC24;
var a,b: integer;
x: real;
begin
write('Nhap a; b: '); readln(a,b);
if a=0 and b=0 then write('Phuong trinh co vo so nghiem');
if a=0 then write('Phuong trinh vo nghiem');
if a<>0 then write('x=',-b/a:1:2);
readln
end.
7 tháng 3 2022
a: Thay m=1 vào pt, ta được:
\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
b: \(\text{Δ}=\left(-m\right)^2-4\left(2m-4\right)\)
\(=m^2-8m+16\)
\(=\left(m-4\right)^2\)
Để phươg trình có hai nghiệm phân biệt thì m-4<>0
hay m<>4
Theo đề, ta có: \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(-m\right)^2-2\left(2m-4\right)\)
\(=m^2-4m+8\)
\(=\left(m-2\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi m=2
24 tháng 3 2020
bn ơi sao nhiều câu 2 thế?
Giải câu 1 : mảnh vườn..
gọi chiều dài mảnh vườn là x m(x>0)
gọi chiều rộng mảnh vườn là y m(y>0)
chu vi mảnh vườn hình chữ nhật đó là : ( x+y).2 =44 \(\Rightarrow\)x+y = 22 \(\Rightarrow\)x=22-y
Theo đề bài ta có : Diện tích mảnh vườn HCN là : (x+3)(x+2)=xy +55 (1)
Giải phương trình (1) : \(xy+2x+3y+6=xy+55\)
\(\Leftrightarrow2x+3y=49\)
Thay x=22-y vào phương trình trên ta có:
\(2\left(22-y\right)+3y=49\)
\(\Leftrightarrow44-2y+3y=49\)
\(\Leftrightarrow y=5\)\(\Rightarrow\)X=17
Vậy chiều dài mảnh vườn là 17 m, chiều rộng mảnh vườn là 5 m
24 tháng 3 2020
Giải câu 2 :phòng học...
Gọi số ghế trong lớp học là x ghế ( x>0)
Gọi số học sinh trong lớp học là y học sinh ( y>0)
Do xếp mỗi ghế 3 hs thì thừa 4 hs k có chỗ nên ta có phương trình (1) : 3x+4=y
Do xếp mỗi ghế 4 học sinh thì thừa ra 2 ghế. nên ta có phương trình (2) : 4(x-2) =y
Từ 2 phương trình trên ta có : 3x+4 = 4(x-2) =y
\(\Leftrightarrow3x+4=4x-8\)
\(\Leftrightarrow3x-4x=-8-4\)
\(\Leftrightarrow-x=-12\)
\(\Leftrightarrow x=12\) \(\Leftrightarrow y=3.12+4=40\)
Vậy trong phòng học có 12 ghế và 40 học sinh
Công thức nghiệm phương trình bậc 2 :
\(ax^2+bx+c=0\)
\(\Delta=b^2-4.a.c\)
Nếu \(x>0\), Phương trình có 2 nghiệm phân biệt
\(X_1=\frac{b+\sqrt{\Delta}}{2a}\) \(X_2=\frac{b-\sqrt{\Delta}}{2a}\)
Nếu \(x< 0,\) Phương trình vô nghiệm
Nếu \(x=0\), Phương trình có nghiệm kép \(X_1=X_2=\frac{-b}{2a}\)
Phương trình bậc 2 có dạng tổng quát
Trong đó a ≠ 0 , a , b là hệ số, c là hằng số
Để giải phương trình bậc 2, tưc là tìm nghiệm x, ta cần tính delta ( KH:
)
- Nếu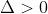
thì phương trình có 2 nghiệm phân biệt
- Nếu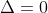
thì phương trình có 1 nghiệm
- Nếu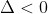
thì phương trình vô nghiệm
* Công thức thu gọn (Áp dụng nếu b là số chẵn)
Ta cần tính
Sau đó lập delta
Xét delta như trường hợp tổng quát
Công thức nghiệm:
* Chú ý : Trong một số trường hợp, các phương trình bậc cao hơn cũng có thể quy về một phương trình bậc hai, nhờ cách đặt ẩn phụ, ví dụ:
Phương trình trùng phương
Đặt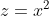
ta được phương trình
Sau đó giải phương trình bậc hai, và suy ra nghiệm x.