Tỉ số 2 góc B và C của tam giác ABC tỉ lệ với 4 : 5. Biết hiệu số đo 2 góc này = 100. Tính số đo 2 góc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CV
27 tháng 9 2016
1/ Ta có \(\frac{C}{5}=\frac{B}{4}=\frac{C-B}{5-4}=\frac{10}{1}\)(tính chất dãy tỉ số = nhau) => \(\hept{\begin{cases}B=10.4=40\\C=10.5=50\end{cases}}\)
2/Gọi diện tích 3 cánh đồng lần lượt là a, b, c( a,b,c >0)
Ta có \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{c-a}{7-3}=\frac{200}{4}=50\)(tính chất dãy tỉ số = nhau) =>\(\hept{\begin{cases}a=50.3=150ha\\b=50.5=250ha\\c=50.7=350ha\end{cases}}\)
30 tháng 3 2023
`a,` Gọi số đo `3` góc của Tam giác `ABC` lần lượt là `x,y,z (x,y,z \ne 0)`
Tỉ lệ thức biểu diễn mối quan hệ giữa số đo `3` góc trong Tam giác `ABC` là `x/2=y/3=z/4`
`b,` Tổng số đo `3` góc trong `1` tam giác là `180^0`
`-> x+y+z=180`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2=y/3=z/4=(x+y+z)/(2+3+4)=180/9=20`
`-> x/2=y/3=z/4=20`
`->x=20*2=40, y=20*3=60, z=20*4=80`
Vậy, số đo của `3` góc trong Tam giác `ABC` lần lượt là `40^0, 60^0, 80^0.`
30 tháng 3 2023
a:
Đặt \(a=\widehat{A};b=\widehat{B};c=\widehat{C}\)
a/2=b/3=c/4
b: a/2=b/3=c/4=(a+b+c)/(2+3+4)=180/9=20
=>a=40; b=60; c=80
AH
Akai Haruma
Giáo viên
21 tháng 8
Lời giải:
Tam giác $ABC$ vuông tại $C$ nên $\widehat{C}=90^0$.
$\widehat{A}+\widehat{B}=180^0-\widehat{C}=180^0-90^0=90^0$
Vì $\widehat{A}, \widehat{B}$ tỉ lệ nghịch với $\frac{1}{2}, \frac{2}{5}$ nên:
$\widehat{A}.\frac{1}{2}=\widehat{B}.\frac{2}{5}$
$\Rightarrow \widehat{A}=\widehat{B}.\frac{2}{5}:\frac{1}{2}=\widehat{B}.\frac{4}{5}$
$\Rightarrow \widehat{A}+\widehat{B}=\frac{9}{5}\widehat{B}$
$\Rightarrow 90^0=\frac{9}{5}\widehat{B}$
$\Rightarrow \widehat{B}=50^0$
$\widehat{A}=90^0-\widehat{B}=90^0-50^0=40^0$
N
3 tháng 12 2021
Gọi số đo ba góc lần lượt là \(a,b,c\left(a,b,c>0\right)\)
Áp dụng tc dtsbn:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{180}{12}=15\)
\(\Rightarrow\left\{{}\begin{matrix}a=45^0\\b=60^0\\c=75^0\end{matrix}\right.\)
CM
2 tháng 6 2018
Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
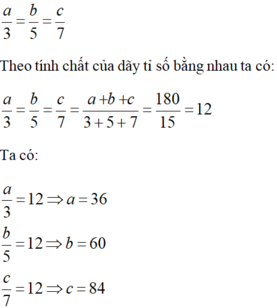
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o
24 tháng 11 2021
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^0}{15}=12^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=36^0\\\widehat{B}=60^0\\\widehat{C}=84^0\end{matrix}\right.\)
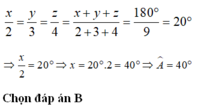
Có: \(\frac{B}{4}=\frac{C}{5}\) và \(C-B=10\)
Áp dụng tc của dãy tỉ số bằng nhau ta có:
\(\frac{B}{4}=\frac{C}{5}=\frac{C-B}{5-4}=\frac{10}{1}=10\)
=> \(\begin{cases}B=40\\C=50\end{cases}\)
Giải:
Ta có: \(\frac{\widehat{B}}{4}=\frac{\widehat{C}}{5}\) và \(\widehat{C}-\widehat{B}=10^o\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{\widehat{B}}{4}=\frac{\widehat{C}}{5}=\frac{\widehat{C}-\widehat{B}}{5-4}=\frac{10^o}{1}=10^o\)
+) \(\frac{\widehat{B}}{4}=10^o\Rightarrow\widehat{B}=40^o\)
+) \(\frac{\widehat{C}}{5}=10^o\Rightarrow\widehat{C}=50^o\)
Vậy \(\widehat{B}=40^o,\widehat{C}=50^o\)