Cho 12+23+...+102=385.Tính S =(0,25)2+(0,5)2+...+(2,5)2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
0
IM
10 tháng 9 2016
Ta có :
\(S=\left(0,25\right)^2+\left(0,5\right)^2+...+\left(2,5\right)^2\)
\(\Rightarrow4S=2^2.\left(0,25\right)^2+2^2.\left(0,5\right)^2+.....+2^2.\left(2,5\right)^2\)
\(\Rightarrow4S=1^2+2^2+....+10^2\)
\(\Rightarrow4S=385\)
\(\Rightarrow S=\frac{385}{4}\)
25 tháng 10 2017
\(a,2^2+4^2+6^2+...+20^2\)
\(=1^2.2^2+2^2.2^2+3^2.2^2+...+10^2.2^2\)
\(=\left(1^2+2^2+3^2+...+10^2\right).2^2\)
\(=385.4\)
\(=1540\)
\(b,\left(0.25\right)^2+\left(0.5\right)^2+...+\left(2.5\right)^2\)
\(=1^2.0,25^2+2^2.0,25^2+...+10^2.0,25^2\)
\(=\left(1^2+2^2+...+10^2\right).0,25^2\)
\(=385.0.0625\)
\(=24.0625\)
25 tháng 10 2017
a/ Có tự ghi lại đề
= ((2+8)+(4+6)+10+(12+18)+(14+16)+20))^2
= ((10+10+10+30+30+20))^2
=(110)^2
=100^2+10^2
=10000+100
=10100
28 tháng 1 2016
Đạt A=2^2+4^2+6^2+...+20^2
A=2^2X(1^2+2^2+3^2+...+10^2) (1)
Mà 1^2+2^2+3^2+...+10^2=385(2)
Thay (2) vào (1), có: A=2^2x385
A=4X385=1540
Vậy 2^2+4^2+6^2+...+20^2 = 1540
TB
26 tháng 9
A=2^2X(1^2+2^2+3^2+...+10^2) (1)
Mà 1^2+2^2+3^2+...+10^2=385(2)
Thay (2) vào (1), có: A=2^2x385
A=4X385=1540
Vậy 2^2+4^2+6^2+...+20^2 = 1540
XD
1
13 tháng 4 2018
\(\text{a)}25\%-\frac{3}{2}+0,5.\frac{12}{5}\)
\(=\frac{1}{4}-\frac{3}{2}+\frac{1}{2}.\frac{12}{5}\)
\(=-\frac{5}{8}+\frac{6}{5}\)
\(=-\frac{25}{40}+\frac{48}{40}\)
\(=\frac{23}{40}\)
\(b)0,25.\frac{7}{3}.30.\text{ }0,5.\frac{8}{45}\)
\(=\frac{1}{4}.\frac{7}{3}.30.\frac{1}{2}.\frac{8}{45}\)
\(=\frac{7}{12}.(30.\frac{8}{90})\)
\(=\frac{7}{12}.\frac{8}{3}\)
\(=\frac{14}{9}\)
\(c)\frac{9}{23}.\frac{5}{8}+\frac{9}{23}.\frac{3}{8}-\frac{9}{23}\)
\(=\frac{9}{23}.\left(\frac{5}{8}+\frac{3}{8}-1\right)\)
\(=\frac{9}{23}.0\)
\(=0\)
ND
1
11 tháng 3 2021
Ta có \(2^2+4^2+...+20^2=2^2\left(1^2+2^2+...+10^2\right)=2^2.385=1540\).
TH
1
AH
Akai Haruma
Giáo viên
8 tháng 5 2023
Lời giải:
$=27\times 2+12,44\times 4+17,56\times 4+23\times 2$
$=2\times (27+23)+4\times (12,44+17,56)$
$=2\times 50+4\times 30$
$=100+120=220$
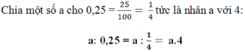
\(S=\left(0,25\right)^2+\left(0,5\right)^2+...+\left(2,5\right)^2\)
\(\Rightarrow\frac{n\left(n+1\right)\left(2n+1\right)}{6}=\frac{2,5\left(2,5+1\right)\left(2,5.2+1\right)}{6}\)
\(\Rightarrow S=8,75\)