sin4α+cos2α+2sin2α.cos2α
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(sin^2\alpha\right)^2+\left(cos^2\alpha\right)^2+2.sin\alpha.cos\alpha\\ =\left(sin^2\alpha+cos^2\alpha\right)^2\\ =\left(1\right)^2=1\)

sin 4 α + cos 4 α + 2 sin 2 α . cos 2 α = sin 2 α + cos 2 α 2 α = 1

Ta có:
`sin^4 \alpha + cos^4 \alpha -sin^6 \alpha- cos^6\alpha`
`=sin^4\alpha+cos^4\alpha-(sin^2\alpha+cos^2\alpha)(sin^4\alpha-sin^2\alpha cos^2\alpha+cos^4\alpha)`
`=sin^4\alpha + cos^4\alpha-(sin^4\alpha-sin^2\alpha cos^2\alpha+cos^4\alpha)`
`=sin^2\alpha cos^2\alpha(ĐPCM)`

cos^4a-sin^4a
=(cos^2a-sin^2a)(cos^2a+sin^2a)
=cos^2a-sin^2a
=cos2a

a: (sina+cosa)^2
=sin^2a+cos^2a+2*sina*cosa
=1+sin2a
b: \(cos^4a-sin^4a=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)\)
\(=cos^2a-sin^2a=cos2a\)

a: VT=sin^2a(sin^2a+cos^2a)+cos^2a
=sin^2a+cos^2a
=1=VP
b: \(VT=\dfrac{sina+sina\cdot cosa+sina-sina\cdot cosa}{1-cos^2a}=\dfrac{2sina}{sin^2a}=\dfrac{2}{sina}=VP\)
c: \(VT=\dfrac{sin^2a+1+2cosa+cos^2a}{sina\left(1+cosa\right)}\)
\(=\dfrac{2\left(cosa+1\right)}{sina\left(1+cosa\right)}=\dfrac{2}{sina}=VP\)
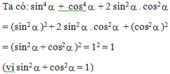
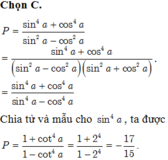
\(=sin^4a+sin^2a.cos^2a+sin^2a.cos^2a+cos^2a\)
\(=sin^2a\left(sin^2a+cos^2a\right)+cos^2a+sin^2a.cos^2a\)
\(=sin^2a+cos^2a+sin^2a.cos^2a\)
\(=1+sin^2a.cos^2a\)
Với lớp 9 thì tới đây có thể coi như không rút gọn tiếp được
\(\sin^4\alpha+2\cdot\sin^2\alpha\cdot\cos^2\alpha+\cos^4\alpha\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)^2\)
=1