2 quả cầu nhỏ bằng kim loại giống nhau , treo trên 2 dây cùng độ dài vào cùng một điểm , được tích điện bằng nhau và cách nhau một đoạn a=5cm . chạm nhẹ tay vào quả cầu (2) . hiện tượng gì xảy ra và tìm khoảng cách giữa chúng sau đó . cho chiều dài dây treo l>a .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 9 2016
Chạm tay vào quả cầu nào thì quả cầu đó sẽ bị mất hết điện tích và hút nhau. Sau đó quả cầu còn điện sẽ truyền điện tích cho quả cầu kia, chúng tích điện như nhau và lại đẩy nhau. Tổng điện tích đã giảm một nửa.
Gọi L là chiều dài dây.
Khoảng cách từ hai điện tích tới điểm treo là h=căn (L2−(a/2)2)
Xét sự cân bằng của 1 điện tích lúc đầu: F=P.tanα=P.a2h
Hay k.q2a2=P.a2h
Lúc sau h′=căn(L2−(a′/2)2)
F=P.tanα′=P.a′2h′
Hay k.q24a′2=P.a′2h′
Dựa vào đó tính a'.
VT
10 tháng 7 2019
Chọn đáp án B
Góc lệch của mỗi quả cầu so với phương thẳng đứng được xác định bởi công thức
VT
14 tháng 10 2018
Đáp án C
Ban đầu góc giữa 2 quả cầu là 60 0 → Khoảng cách giữa 2 quả cầu là l (với l là chiều dài sợi dây)
Lực đẩy giữa 2 quả cầu là F = k q 1 q 2 l 2
Xét trạng thái cân bằng lực của 1 quả cầu ta có
Khi 2 quả cầu tiếp xúc nhau thì điện tích của 2 quả cầu sẽ được chia đều
Khi đó mỗi quả cầu sẽ tích điện là q 1 + q 2 2
Lúc này góc giữa 2 quả cầu là 90° nên khoảng cách giữa 2 quả cầu là l ' = l 2
Lực đẩy tĩnh điện giữa 2 quả cầu là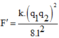 
Xét trạng thái cân bằng lực ta có
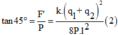
Chia (1) cho (2) ta có
. Đặt tỉ số 
Giải phương trình bậc 2 này là tìm ra 2 giá trị
x = 11,77 hoặc x = 0,085
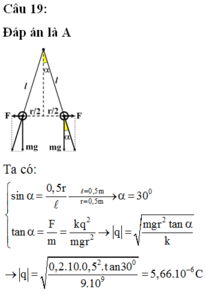
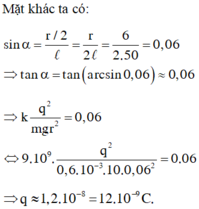
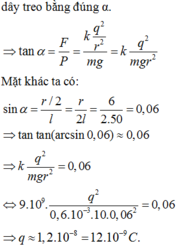
\(F=P\tan a=P\frac{R}{2l}\)
\(F'=P\tan a'=P\frac{R'}{2l}\)
Với l là chiều dài sợi dây
\(F=\frac{kq^2}{R^2},F'=\frac{kq^2}{4R^2}\)
Lập tỉ số (tự lập)
\(4R'^3=R^3\Rightarrow R'=\frac{R}{\sqrt[3]{4}}=3,15\)(cm)
sao 4R^3=R^3