cho a và b là 2 số thục dương và thỏa mãn a+b<1. Tìm GTNN của BT \(A=\frac{a^2}{1-a}+\frac{b^2}{1-b}+\frac{1}{a+b}+a+b\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


m.n/(m^2+n^2 ) và m.n/2018
- Đặt (m,n)=d => m= da;n=db ; (a,b)=1
=> d^2(a^2+b^2)/(d^2(ab)) = (a^2+b^2)/(ab) => b/a ; a/b => a=b=> m=n=> ( 2n^2+2018)/n^2 =2 + 2018/n^2 => n^2/2018
=> m=n=1 ; lẻ và nguyên tố cùng nhau. vì d=1
Vẽ SH _I_ (ABCD) => H là trung điểm AD => CD _I_ (SAD)
Vẽ HK _I_ SD ( K thuộc SD) => CD _I_ HK => HK _I_ (SCD)
Vẽ AE _I_ SD ( E thuộc SD).
Ta có S(ABCD) = 2a² => SH = 3V(S.ABCD)/S(ABCD) = 3(4a³/3)/(2a²) = 2a
1/HK² = 1/SH² + 1/DH² = 1/4a² + 1/(a²/2) = 9/4a² => HK = 2a/3
Do AB//CD => AB//(SCD) => khoảng cách từ B đến (SCD) = khoảng cách từ A đến (SCD) = AE = 2HK = 4a/3

Thế b=9a vào đẳng thức còn lại ta được
a 9 a = ( 9 a ) a ⇒ ( a 9 ) a ⇒ a 9 = 9 a ⇒ a 8 = 9 ( do a > 0)
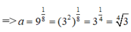
Chọn đáp án B

c1:áp dụng bđt AM-GM:
\(a+b\ge2\sqrt{ab}\Rightarrow ab\le\left(\dfrac{a+b}{2}\right)^2=1008^2\)
=> đáp án A
c2: tương tự c1 . đáp án b
3.
\(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{ab}{ab}}=2\)
Đáp án A
4.
\(a^2-a+1=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) ;\(\forall a\)
Đáp án A

Đáp án A
Ta có P = 1 2 . 1 - log a b log a b - 1 2 = 1 - 2 2 2 - 1 .

Đổi về cơ số a có
log a b a b = log a a b log a a b = 1 2 1 + log a b 1 - log a b = 1 2 ( 1 + 2 ) 1 - 2 = - 3 2
Chọn đáp án A.

Ta có:

Dấu “=” xảy ra khi và chỉ khi


Vậy số bộ a,b,c thỏa mãn điều kiện đã cho là 1.
Chọn B.

Chọn D
Cách 1: Cho a= 4; b= 2 ta thấy log24> 1> log42
Cách 2: Ta có: 1< a< b nên

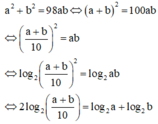
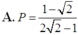
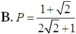
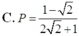
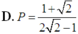
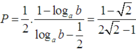
ta có :
\(A=\frac{a^2}{1-a}+a+\frac{b^2}{1-b}+b+\frac{1}{a+b}=\frac{a}{1-a}+\frac{b}{1-b}+\frac{1}{a+b}\)
\(A=\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{a+b}-2\)
mà : \(\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{a+b}\ge\frac{9}{1-a+1-b+a+b}=\frac{9}{2}\)
Vậy \(A\ge\frac{9}{2}-2=\frac{5}{2}\)
dấu bằng xảy ra khi : \(1-a=1-b=a+b\Leftrightarrow a=b=\frac{1}{3}\)