Question

[M Thiện Nguyễn]

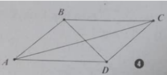
Câu 1: Cho hình bình hành ABCD. Phép tịnh tiến \(T_{\overrightarrow{DA}}\) biến

A. B thành C

B. C thànhB

C. C thành A

D. A thành D

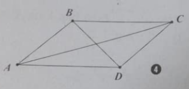
Câu 2: Cho hình bình hành ABEF. Gọi D,C lần lượt là trung điểm của AF và BF, O là giao điểm của AC và BD, I là giao điểm của FC và DE. Phép tịnh tiến \(T_{\overrightarrow{FI}}\) biến tam giác DIF thành tam giác nào sau đây:

A. \(\Delta AOD\)

B. \(\Delta CIE\)

C. \(\Delta OBC\)

D. \(\Delta OCI\)

Câu 3: Trong mặt phẳng, phép tịnh tiến \(T_{\overrightarrow{v}}\left(A\right)=B\) và \(T_{\overrightarrow{v}}\left(C\right)=D\)  với \(\left(\overrightarrow{v}\ne\overrightarrow{0}\right)\) Mệnh đề nao sau đây sai?

A. \(\overrightarrow{AC}=\overrightarrow{BD}\)

B. \(\overrightarrow{AB}=\overrightarrow{CD}\)

C. \(\overrightarrow{AD}=\overrightarrow{CB}\)

D. \(AB=CD\)

Câu 4: Trong mặt phẳng tọa độ Oxy cho \(\overrightarrow{v}=\left(3;1\right)\). Tìm tọa độ của điểm \(M'\) là ảnh của điểm \(M\left(-2;1\right)\) qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\)

A. \(M'\left(5;0\right)\)

B. \(M'\left(1;2\right)\)

C. \(M'\left(-5;0\right)\)

D. \(M'\left(5;2\right)\)

Câu 5: Trong mặt phẳng tọa độ Oxy cho điểm \(M\left(-2;1\right)\). Tìm tọa độ điểm N sao cho M là ảnh của N qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}=\left(-3;2\right)\) 

A. N(1;3)

B. N(1;-1)

C. N(-1;-1)

D. N(-5;3)

Câu 6: Trong mặt phẳng tọa độ Oxy, cho hai điểm M(2;3) và N(1;-1). Phép tịnh tiến theo véc tơ \(\overrightarrow{v}\) biến điểm M thành điểm N. Khi đó ta có:

A.\(\overrightarrow{v}=\left(3;2\right)\)

B. \(\overrightarrow{v}=\left(-1;-4\right)\)

C. \(\overrightarrow{v}=\left(1;4\right)\)

D. \(\overrightarrow{v}=\left(-3;2\right)\)

Câu 7: Trong mặt phẳng Oxy và đường tròn \(\left(C\right):x^2+y^2-2x+4y-4=0\).  Viết phương trình đường tròn (C') là ảnh của (C) qua \(T\overrightarrow{v}\)

A. \(\left(x-4\right)^2+\left(y-1\right)^2=4\)

B. \(\left(x+4\right)^2+\left(y+1\right)=9\)

C. \(\left(x-4\right)^2+\left(y-1\right)^2=9\)

D. \(x^2+y^2+8x+2y-4=0\)

Câu 8: Trong mặt phẳng tọa độ, xác định của đường thẳng \(\left(d\right):x+y-2=0\) qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}=\left(-3;0\right)\)

A. x+y+3=0

B. x-y-2=0

C. x+y+2=0

D. x+y+1=0