Con lắc lò xo dao động tắt dần, lò xo có độ cứng k = 40 N/m, ban đầu ở vị trí biên có biên độ A0,
khi qua vị trí cân bằng một lần đến vị trí biên, biên độ còn là A1, đoạn đường đi được là s = A1 + A0 = 9
cm. So với ban đầu, cơ năng giảm 1,8.10-2 J thì biên độ ban đầu là
A. A0 = 4 cm. B. A0 = 5,2 cm. C. A0 = 5 cm. D. A0 = 5,8 cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
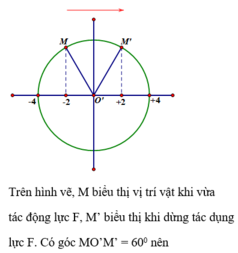
Khi chưa có lực F , vị trí cân bằng của vật là O . Biên độ là : A = 2 3 c m
Khi có thêm lực F, vị trí cân bằng dịch chuyển đến O’ sao cho : OO' = F k = 0 , 02 m = 2 c m
ω = k m = 10 π rad / s ⇒ T = 0 , 2 s
Khi F bắt đầu tác dụng (t=0), vật đến O có li độ so với O’ là : x 1 = - 2 c m và có vận tốc v 1 = ω A = 20 π 3 cm / s
Biên độ : A 1 = x 1 2 + v 1 ω 2 = 4 c m
Thời gian ngắn nhất vật đi từ O đến O’ là: t 1 = T 60 = 1 60 s
Ta thấy rằng t = 1 30 s = 2 t 1 nên khi F ngừng tác dụng thì vật có li độ so với O là x 2 = 4 c m và có vận tốc v 2 = v 1 = ω A = 20 π 3 cm / s
Từ đó biên độ từ lúc ngừng tác dụng lực là :
A 2 = x 2 2 + v 2 ω 2 = 2 7 c m
Vậy A 1 A 2 = 2 7

Đáp án B
Tần số góc của dao động ω = k m = 10 rad/s → T = 0,2 s.
→ Tốc độ của vật khi đi qua vị trí cân bằng v = v m a x = ω A = 20 3 cm/s.
+ Dưới tác dụng của ngoại lực con lắc dao động quanh vị trí cân bằng mới O′, tại vị trí này lò xo giãn một đoạn O O ' = Δ l 0 = F k = 2 100 = 2 cm.
+ Tại ví trí xuất hiện ngoại lực, con lắc có x ' = - 2 cm, v ' = v m a x
→ Biên độ dao động của con lắc lúc này A 1 = x ' 2 + v ' ω = 2 2 + 20 3 10 2 = 4 cm.
+ Ta chú ý rằng con lắc dao động quanh vị trí cân bằng mới O′ trong khoảng thời gian Δ t = T 6 = 1 30 s, sau khoảng thời gian này, vật có x 1 = 0 , 5 A 1 , v 1 = 3 v 1 m a x 2 = 3 ω A 1 2 = 3 10 π .4 2 = 20 3 π cm/s.
→ Ngừng lực tác dụng F, con lắc lại dao động quanh vị trí cân bằng cũ, lúc này con lắc có x ′ = O O ′ + 0 , 5 A 1 = 4 c m , v ' = v 1 = 20 3 π cm/s.
→ Biên độ dao động mới A 2 = x ' 2 + v ' ω 2 = 4 2 + 20 3 π 10 π 2 = 2 7 cm.
→ Vậy A 1 A 2 = 4 2 7 = 2 7

Chọn B
+ ω = k m = 1600 1 = 40 rad/s.
+ Truyền cho vật vận tốc 2 m/s tại vị trí cân bằng => vmax = ωA = 2 => A = 0,05m = 5cm.

Đáp án A
Phương pháp: Áp dụng định luật bảo toàn cơ năng
Cách giải:
Ta có
![]()
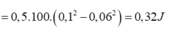

Đáp án A
Độ cứng của các lò có sau lần đầu tiên và lần thứ hai giữ cố định lần lượt là
![]()
+Sau lần 1 (lúc nhốt x=0,8A) thế năng bị nhốt và cơ năng còn lại lần lượt là
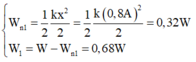
+Sau lần 2 (lúc nhốt x=0,5A1) thế năng bị nhốt và cơ năng còn lại lần lượt là

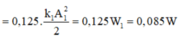
Mà
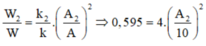
![]()

Đáp án A
Độ cứng của các lò có sau lần đầu tiên và lần thứ hai giữ cố định lần lượt là k 1 = 2 k = 36 N / m và k 2 = 4 k = 72 N / m
Sau lần 1 (lúc nhốt x = 0,8 A ) thế năng bị nhốt và cơ năng còn lại lần lượt là
W n 1 = 1 2 k x 2 2 = 1 2 k 0,8 A 2 2 = 0,32 W W 1 = W − W n 1 = 0,68 W
Sau lần 2 (lúc nhốt x = 0,5 A 1 ) thế năng bị nhốt và cơ năng còn lại lần lượt là
W n 2 = 1 2 k 1 x 1 2 2 = 1 2 k 1 0,5 A 1 2 2 = 0,125. k 1 A 1 2 2 = 0,125 W 1 = 0,085 W W 2 = W 1 − W n 2 = 0,595 W
Mà W 2 W = k 2 k . A 2 A 2 ⇒ 0,595 = 4. A 2 10 2 ⇒ A 2 ≈ 3,86 ( c m )

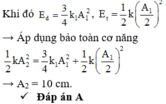



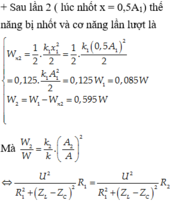
\(E_0-E_1=\frac{1}{2}k\left(A^2_0-A^2_1\right)=\frac{1}{2}k\left(A_0-A_1\right)\left(A_0+A_1\right)=1,8.10^{-2}\)
\(\Rightarrow A_0-A_1=0,01\)
Kết hợp với \(A_0+A_1=0,09\)
Vậy \(A_0=5cm;A_1=4cm\)
Chọn C
chon C