Cho ΔABC cân tại A có AB =AC =13cm ,BC =10cm .Tính cos góc A.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm
=>cosBAH=AH/AB=12/13
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)

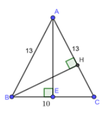
Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến
=> E là trung điểm BC => EB = EC = 5
Xét ABE vuông tại E có:
![]()
![]()
Mặt khác:
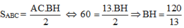
Xét ABH vuông tại H có:
![]()
Đáp án cần chọn là: A

a: XétΔADB và ΔADC có
AD chung
DB=DC
AB=AC
Do đó: ΔABD=ΔACD
b: ta có: ΔABC cân tại A
mà AD là trung tuyến
nên AD là đường cao
c: BD=BC/2=5cm
nên AD=12cm

a) Sửa đề: Cm AG vuông góc với BC
Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AN=NB=AM=MC
Xét ΔNBC và ΔMCB có
NB=MC(cmt)
\(\widehat{NBC}=\widehat{MCB}\)(hai góc ở đáy của ΔABC cân tại A)
BC chung
Do đó: ΔNBC=ΔMCB(c-g-c)
Suy ra: \(\widehat{NCB}=\widehat{MBC}\)(hai góc tương ứng)
hay \(\widehat{GBC}=\widehat{GCB}\)
Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)(cmt)
nên ΔGBC cân tại G(Định lí đảo của tam giác cân)
Suy ra: GB=GC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: GB=GC(cmt)
nên G nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AG là đường trung trực của BC
hay AG\(\perp\)BC(đpcm)

- Áp dụng định lý pi ta go vào tam giác ABC vuông tại A ta được :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC^2+5^2=13^2\)
\(\Rightarrow AC=12\left(cm\right)\)
- Xét tam giác BHA và tam giác BAC có : \(\left\{{}\begin{matrix}\widehat{BHA}=\widehat{BAC}=90^o\\\widehat{B}\left(chung\right)\end{matrix}\right.\)
=> Hai tam giác trên đồng dạng .
=> \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
=> \(BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\)
=> \(CH=BC-BH=\dfrac{144}{13}\left(cm\right)\)
- Áp dụng định lý pi ta go vào tam giác ABH vuông tại H ta được :
\(AH^2+BH^2=AB^2\)
\(\Rightarrow AH=\dfrac{60}{13}\left(cm\right)\)
Vậy ...

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔAHB=ΔAHC
nên HB=HC
=>HB=BC/2=6(cm)
Xét ΔAHB vuông tại H có
\(AB^2=AH^2+BH^{ }\)
hay AH=8(cm)
c: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của AB
Do đó: MN là đường trung bình
=>MN//BC
d: Xét ΔNCB và ΔMBC có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó: ΔNCB=ΔMBC
Suy ra: \(\widehat{GCB}=\widehat{GBC}\)
hay ΔGBC cân tại G

tự vẽ hình nhé Gọi E là trung điểm của CD.
Xét tam giác BDC ta có:
M là trung điểm của BC ( gt )
E là trung điểm của CD (cách vẽ)
=> EM là đường trung trực của tam giác BDC.
=> EM // BD => EM // ID ( I thuộc BD )
Xét tam giác AME có:
I là trung điểm của AM (gt)
EM // ID (cmt)
=> D là trung điểm của AE
Xét tam giác AME có:
I là trung điểm của AM (gt)
D là trung điểm của AE (cmt)
=> ID là đường trung bình của tam giác AME.
⇒ID=12ME⇒ID=12ME
Mà ME=12BDME=12BD ( ME là đường trung bình của tam giác BDC )
Nên ID=14BD(1)ID=14BD(1)
Xét tam giác ABC vuông tại A ta có:
BC2 = AB2+AC2 ( Định lý Pitago thuận)
Thay:
132 = 52 + AC2
169 = 25 + AC2 => AC2 = 169 - 25 = 144
=> AC2 = 122
=> AC = 12 (cm)
Ta có: AD = ED ( D là trung điểm của AE )
ED = EC ( E là trung điểm của DC)
=> AD = ED = EC
Mà AD + ED + EC = AC (gt)
Nên: AD + AD + AD = AC
=> 3AD = AC
=> AD = AC/3
Mặt khác AC = 12 cm (cmt)
=> AD = 12/3 = 4 (cm)
Xét tam giác ABD vuông tại A ta có:
BD2 = AB2+AD2 ( định lý Pitago thuận)
BD2 = 52+42
BD2 = 25 + 20
BD2 = 45
=> BD=√45⇒BD=3√5(cm)(2)BD=45⇒BD=35(cm)(2)
Thế (2) vào (1) ta được:
ID=3√54(cm)(3)ID=354(cm)(3)
Ta có:
BI + ID = BD ( I thuộc BD )
=> BI = BD - ID (4)
Thế (2), (3) vào (4) ta được:
BI=3√5−3√54BI=35−354
BI=3√5(1−14)BI=35(1−14)
BI=3√5.34BI=35.34
BI=9√54(cm)

Áp dụng định lí Py-ta-go vào tam giác ABC vuông tại A, ta có:
\(AB^2+AC^2=BC^2\\ AC^2=BC^2-AB^2\\ AC^2=13^2-5^2\\ AC^2=169-25\\ AC^2=144\\ AC=12\left(cm\right)\)

A/Vì AH vuông góc BC,mà TG ABC cân nên vừa là đường cao vừa là đường trung tuyến.
(Bạn có thể làm nhiều cách để giải thích rõ hơn chẳng hạn)
=>H là trung điểm của BC (t/c đường trung tuyến)
b/Ta có:BC=BH=CH=>CH=10:2=5(cm)
Mà ABC là TG cân =>AB=AC=13(cm)
Trong TG ACH:AH2=AC2-CH2(đ/ lí đảo Pytago)
AH2=132-52
=>AH2=122
=>AH=12(cm)
A B C H K Từ A kẻ đường cao AH vuông góc với BC tại H.
Từ B kẻ đường cao BK vuông góc với AC tại K
Khi đó, ta có BH = HC = 1/2BC = 5 (cm)
\(AH=\sqrt{AC^2-\left(\frac{BC}{2}\right)^2}=13^2-5^2=12\left(cm\right)\)
Dễ thấy hai tam giác HCA và KCB đồng dạng (g.g)
Suy ra \(\frac{HC}{KC}=\frac{AC}{BC}\) hay \(\frac{5}{KC}=\frac{13}{10}\Rightarrow KC=\frac{50}{13}\Rightarrow AK=AC-KC=13-\frac{50}{13}=\frac{119}{13}\left(cm\right)\)
Xét tam giác AKB, ta có :
\(CosA=\frac{AK}{AC}=\frac{\frac{119}{13}}{13}=\frac{119}{169}\)
kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm
=>cosBAH=AH/AB=12/13
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)