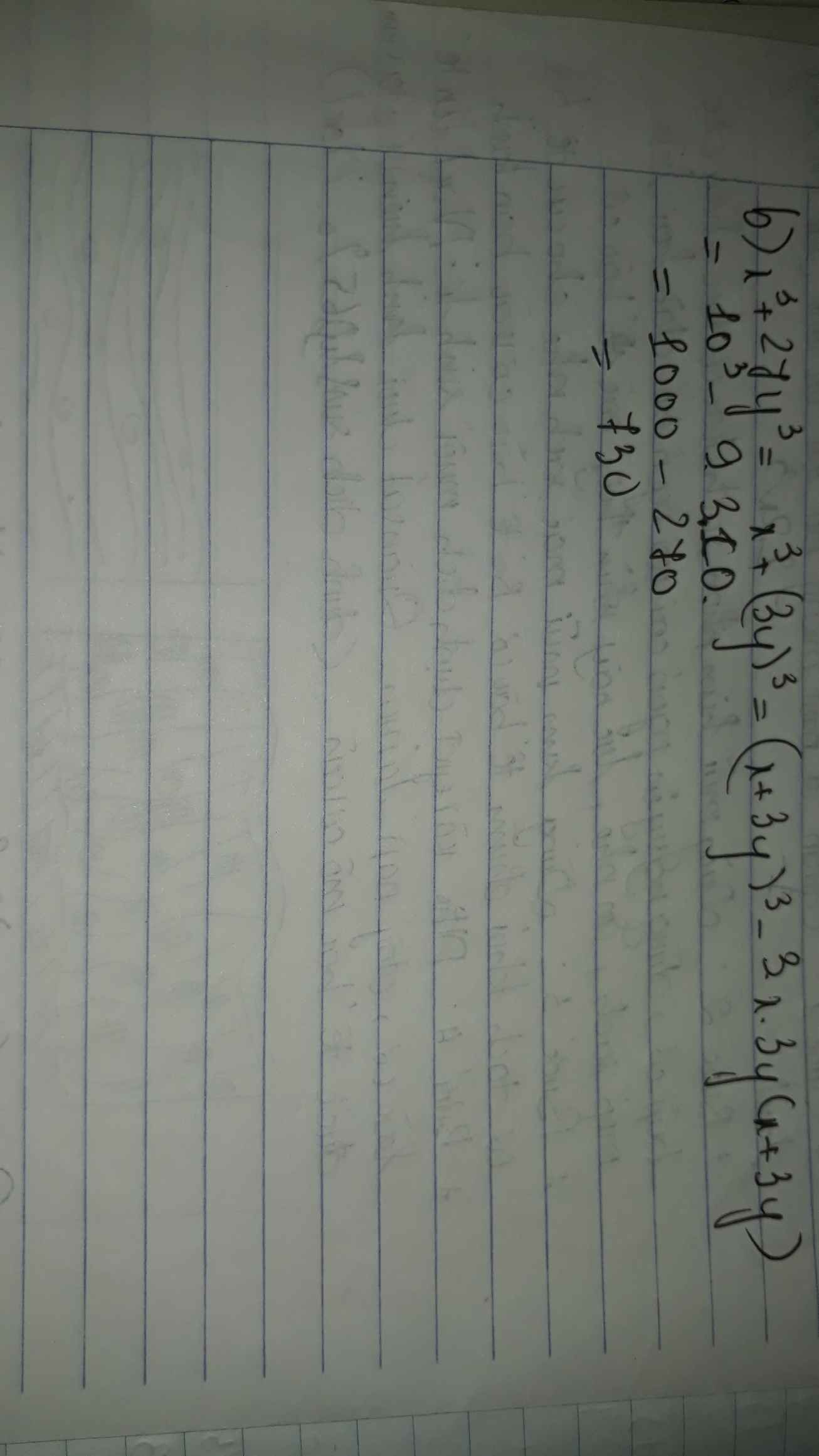Làm tính chia: (x^{3}-27y^{3}) : (x-3y) =(x3−27y3):(x−3y)=
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Ta có: \(x-2y=-4\Rightarrow\left(x-2y\right)^2=16\)
\(\Rightarrow x^2-4xy+4y^2=16\Rightarrow x^2+4y^2=16+4xy=16+4.6=40\)
\(x^3-8y^3=\left(x-2y\right)\left(x^2+2xy+4y^2\right)=\left(-4\right)\left(40+2.6\right)=-208\)
b) Ta có: \(x+3y=10\Rightarrow x^2+6xy+9y^2=100\Rightarrow x^2+9y^2=100-6xy=100-6.3=82\)
\(x^3+27y^3=\left(x+3y\right)\left(x^2-3xy+9y^2\right)=10\left(82-3.3\right)=730\)

\(x^3+27y^3=1-9xy\left(x+3y\right)\)
<=> \(x^3+27y^3+9xy\left(x+3y\right)=1\)
<=> \(\left(x+3y\right)^3=1\)
<=> \(x+3y=1\)
Vậy \(M=1\)
\(x^3+27x^3=1-9xy\left(x+3y\right)\))
\(=\left(x+3y\right)\left(x^2-3xy+9y^2\right)=1-9xy\left(x+3y\right)\)
=\(\left(x+3y\right)\left(x^2-3xy+9y^2\right)-1+9xy\left(x+3y\right)=0\)
=\(\left(x+3y\right)\left(x^2-3xy+9y^2+9xy\right)-1=0\)
=\(\left(x+3y\right)\left(x^2+6xy+9y^2\right)-1=0\)
=\(\left(x+3y\right)\left(x+3y\right)^2-1=0\)
=\(\left(x+3y\right)\left(x+3y\right)^2=1\)
\(\Rightarrow x+3y=\left(x+3y\right)^2=1\)
\(\Rightarrow x+3y=1\)

\(1.\)
\(a.\)
\(\left(x-3\right)\left(x^2+3x+9\right)-\left(54+x^3\right)\)
\(=\left(x^3-3^3\right)-\left(54+x^3\right)\)
\(=x^3-27-54-x^3\)
\(=-81\)
\(b.\)
\(\left(3x+y\right)\left(9x^2-3xy+y^2\right)-\left(3x-y\right)\left(9x^2+3xy+y^2\right)\)
\(=\left(27x^3+y^3\right)-\left(27x^3-y^3\right)\)
\(=27x^3+y^3-27x^3+y^3\)
\(=2y^3\)
\(2.\)
\(a.\)
\(\left(x+3y\right)\left(x^2-3xy+9y^2\right)=x^3+27y^3\)
\(b.\)
\(\left(2x-3y\right)\left(4x^2+6xy+9y^3\right)=8x^3-27y^3\)
1) a) \(\left(x-3\right)\left(x^2+3x+9\right)-\left(54+x^3\right)\)
\(=\left(x^3-3^3\right)-\left(54+x^3\right)\\ =\left(x^3-27\right)-54-x^3\\ =-27-54\\ =-81\)
b) \(\left(3x+y\right)\left(9x^2-3xy+y^2\right)-\left(3x-y\right)\left(9x^2+3xy+y^2\right)\)
\(=\left[\left(3x\right)^3+y^3\right]-\left[\left(3x\right)^3-y^3\right]\\ =2y^3\)
2) a) \(\left(x+3y\right)\left(x^2-3xy+9y^2\right)=x^3+27y^3\)
b) \(\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)=8x^3-27y^3\)

a: \(=-8x^5+6x^3-2\)
b: \(=-\dfrac{2}{3}x+7-x^2y\)
c: \(=\dfrac{7\left(x-y\right)^4+4\left(x-y\right)^3}{\left(x-y\right)^2}=7\left(x-y\right)^2+4\left(x-y\right)\)
d: \(=\dfrac{6\left(x-3y\right)^4}{5\left(x-3y\right)}=\dfrac{6}{5}\left(x-3y\right)^3\)

ĐK: \(\hept{\begin{cases}x\ge2\\y\ge-\frac{1}{3}\end{cases}}\)
\(\sqrt{x-2}+x^3-6x^2+12x=\sqrt{3y+1}+27y^3+27y^2+9y+9\)
<=> \(\sqrt{x-2}+x^3-6x^2+12x-8=\sqrt{3y+1}+27y^3+27y^2+9y+1\)
<=> \(\sqrt{x-2}+\left(x-2\right)^3=\sqrt{3y+1}+\left(3y+1\right)^3\)
<=> \(\left(\sqrt{x-2}-\sqrt{3y+1}\right)+\left[\left(x-2\right)^3-\left(3y+1\right)^3\right]=0\)
<=> \(\frac{x-3y-3}{\sqrt{x-2}+\sqrt{3y+1}}+\left(x-3y-3\right)\left[\left(x-2\right)^2+\left(x-2\right)\left(3y+1\right)+\left(3y+1\right)^2\right]=0\)
<=> \(\left(x-3y-3\right)\left(\frac{1}{\sqrt{x-2}+\sqrt{3y+1}}+\left(x-2\right)^2+\left(x-2\right)\left(3y+1\right)+\left(3y+1\right)^2\right)=0\)
<=> \(x-3y-3=0\)
vì \(\frac{1}{\sqrt{x-2}+\sqrt{3y+1}}+\left(x-2\right)^2+\left(x-2\right)\left(3y+1\right)+\left(3y+1\right)^2>0\)
<=> x = 3y + 3
Thế vào phương trình trên ta có:
\(2+2\left(3y+3\right)^2-2y^2+3\left(3y+3\right)y-4\left(3y+3\right)-3y=0\)
<=> \(25y^2+30y+8=0\Leftrightarrow\orbr{\begin{cases}y=-\frac{2}{5}\\y=-\frac{4}{5}\end{cases}}\)không thỏa mãn đk
Vậy hệ vô nghiệm.