Một con lắc lò xo treo thẳng đứng, đưa vật đến vị trí lò xo không biến dạng rồi buông nhẹ, vật dao động điều hoà. Khi vật đi qua vị trí cân bằng thì có tốc độ là 25\(\pi\) cm/s. Lấy g = 10 m/s2 ; \(\pi\)2 = 10. Biên độ dao động bằng bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SS
24 tháng 7 2016
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)
VT
27 tháng 12 2019
+ Nâng vật đến vị trí lò xo không giãn rồi thả nhẹ, con lắc sẽ dao động với biên độ A = Δ l 0 .
→ Áp dụng công thức độc lập thời gian :
A 2 = x 2 + v 2 ω 2 → ω 2 = g Δ l 0 A = Δ l 0 A 2 − v 2 g A − x 2 = 0 → A = 5 c m .
+ Tại thời điểm thả vật, vật đang ở vị trí x = – A , sau khi đi được quãng đường S = 5 A + 0 , 5 A = 27 , 5 c m vật đi đến vị trí x = + 0 , 5 A → gia tốc của vật khi đó có độ lớn là
a = ω 2 x = g Δ l 0 A 2 = g 2 = 5 . m / s 2
Chọn đáp án C
VT
5 tháng 1 2019
+ Nâng vật đến vị trí lò xo không giãn rồi thả nhẹ, con lắc sẽ dao động với biên độ A = Δ l 0
→ Áp dụng công thức độc lập thời gian :
→ A 2 = x 2 + v 2 ω 2 → ω 2 = g Δ l 0 A = Δ l 0 A 2 − v 2 g A − x 2 = 0 → A = 5 c m .
+ Tại thời điểm thả vật, vật đang ở vị trí x = – A , sau khi đi được quãng đường S = 5 A + 0 , 5 A = 27 , 5 c m vật đi đến vị trí x = + 0 , 5 A → gia tốc của vật khi đó có độ lớn là a = ω 2 x = g Δ l 0 A 2 = g 2 = 5 . m / s 2
Đáp án C
VT
6 tháng 4 2018
Đáp án C
+ Vị trí lò xo không giãn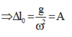 
+ x và v vông pha với nhau nên :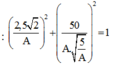
+ Sau 27,5cm vật ở vị trí |x| = 2,5 cm , x và a ngược pha nhau nên suy ra :
VT
17 tháng 3 2017
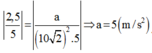
Chọn đáp án C
Nâng vật đến vị trí lò xo không giãn rồi thả nhẹ, con lắc sẽ dao động với biên độ A = ∆ l 0 .
→ Áp dụng công thức độc lập thời gian:
+ Tại thời điểm thả vật, vật đang ở vị trí x = –A, sau khi đi được quãng đường S = 5A + 0,5A = 27,5 cm vật đi đến vị trí x = +0,5A
→
gia tốc của vật khi đó có độ lớn là 
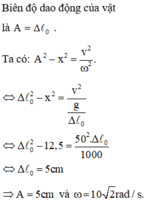
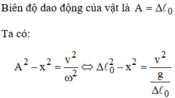
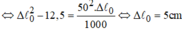
Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)