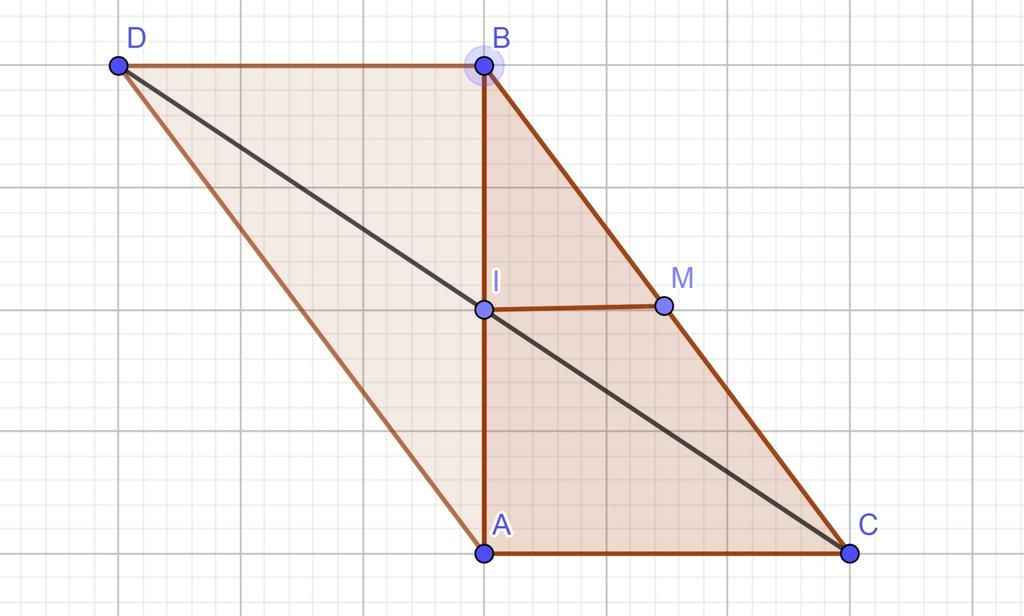
Cho tam giac ABC vuông tại A,AC =5cm và AB=12cm,I là trung điểm của AB,D đối xứng với C qua I.
a) Tứ giác ADBC là hình gì ? vì sao?
b) Gọi M là trung điểm của BC.Chứng minh MI vuông góc với AB.
c) Tính độ dài AM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
R
5 tháng 2 2022
a) Xét tứ giác \(ADBC\) ta có :
\(IB=IA\left(g.t\right)\)
\(IC=IC\) ( \(D\) đối xứng qua \(I\))
Vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Vậy tứ giác \(ADBC\) là hình bình hành
b) Xét \(\Delta ABC\) ta có :
\(IA=IB\left(g.t\right)\)
\(MB=MC\left(g.t\right)\)
\(\Rightarrow IM\) là đường trung bình \(\Delta ABC\)
Do đó : \(IM\text{/ / }AC\)
Mà \(AB\text{⊥}AC\left(A=90^o\right)\)
Vậy \(IM\text{⊥}AB\)
Áp dụng định lí pytago \(\Delta ABC\) ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{13^2-5^2}=12\left(cm\right)\)
\(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.13.5=30\left(cm^2\right)\)
VL
24 tháng 11 2023
Phần tính diện tích ∆ABC cậu lộn AB =13cm roii í phải là 1/2 × 12 × 5 = 30 cm nha
8 tháng 1 2020
hình bạn tự vẽ nhé
a) Xét tứ giác ADBC có AB giao DC tại I là trung điểm của mỗi đường
\(\Rightarrow ADBC\)là hình bình hành (dhnb)
b) Xét tam giác ABC có:
I là trung điểm của AB (gt) , M là trung điểm của BC(gt)
\(\Rightarrow IM\)là đường trung bình tam giác ABC
\(\Rightarrow IM//AC\left(tc\right)\)
Mà \(AB\perp AC\)
\(\Rightarrow IM\perp AB\)( từ vuông góc đến song song )
c) Áp dụng định lý Py-ta-go vào tam giác ABC ta được:
\(AB^2+AC^2=BC^2\)
\(AB^2+5^2=13^2\)
\(AB^2=144\)
\(\Rightarrow AB=12\left(cm\right)\)
\(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}.12.5=30\left(cm^2\right)\)
Vậy ...
6 tháng 2 2022
a: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=30\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của BC
I là trung điểm của AB
Do đó: MI là đường trung bình
=>MI//AC
hay MI⊥AB
c: Xét tứ giác ACBD có
I là trung điểm của AB
I là trung điểm của CD
Do đó: ACBD là hình bình hành
TD
6 tháng 2 2022
a/ Áp dụng Pytago vào ΔABC, ∠A=90 độ
⇒AB²=BC²-AC²
⇒AB²= 13²-5²
⇒AB²=144
⇒AB=12 (cm)
Vậy diên tích tam giác ABC:
SΔABC=1212 ×AB×AC=1212 ×12×5=30 (cm²)
b/
b/ Ta có :
IB=IA(gt)
MB=MC (gt)
⇒IM là đường trung bình ΔABC
⇒IM // AC
Và ∠A =90 độ
⇒∠BIM = 90 độ ( đồng vị)
c)
Ta có:
IB=IA (gt)
IC=ID (gt)
⇒ Tứ giác ADBC là hình bình hành ( Theo tính chất hình bình hành)
2 tháng 1 2023
a: D đối xứng M qua AB
nên AD=AM; BD=BM và DM vuông góc với AB
Xét tứ giác AIDE có
góc AID=góc AED=góc EAI=90 độ
Do đó: AIDE là hình chữ nhật
b: AD=AM
BD=BM
mà AD=BD
nên AD=AM=BD=BM
=>ADBM là hình thoi
c: AI=AB/2=3cm
AE=AC/2=4,5cm
SAIDE=3*4,5=13,5cm2
a)ID=IC ;IA=IB => Tứ giác ADBC là hình bình hành.
b)MB=MC
IB=IA
=>MI là đường trung bình của tam giác ABC
=>MI//AC
=>góc BIM=góc A = 90 độ (đồng vị)
hay MI vuông góc với AB tại I
Câu c nè bạn:
ÁP dụng định lý Py-ta-go vào tam giác vuông ABC có:
AB2+AC2=BC2
Và bạn sẽ tính ra được BC=13
Vì tam giác ABC là tam giác vuông lại có AM là đường trung tuyến nên trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền
SUy ra: AM=1/2.BC=1/2.13=6.5