Chứng minh rằng:
\(\alpha,999...=\alpha+1\) với mọi \(\alpha\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
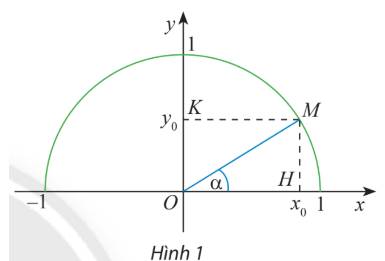
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 6 2020
Coi BPT là bậc 2 với tham số \(sina;cosa\)
Đặt \(f\left(x\right)=\left(1+sin^2a\right)x^2-2\left(sina+cosa\right)x+1+cos^2a\)
Ta có: \(1+sin^2a>0;\forall a\)
\(\Delta'=\left(sina+cosa\right)^2-\left(1+sin^2a\right)\left(1+cos^2a\right)\)
\(=sin^2a+cos^2a+2sina.cosa-1-sin^2a-cos^2a-sin^2a.cos^2a\)
\(=-sin^2a.cos^2a+2sina.cosa-1\)
\(=-\left(sina.cosa-1\right)^2=-\left(\frac{1}{2}sin2a-1\right)^2\)
\(=-\left(\frac{sin2a-2}{2}\right)^2\)
Do \(sin2a-2< 0;\forall a\Rightarrow\left(\frac{sin2a-2}{2}\right)^2>0;\forall a\)
\(\Rightarrow\Delta'< 0;\forall a\Rightarrow f\left(x\right)>0\) với mọi x và a
= cosα; 
= 
= sinα;
BT
11 tháng 5 2017
Ta có:
\(\dfrac{sin\alpha+tan\alpha}{cos\alpha+cot\alpha}=\dfrac{sin\alpha+\dfrac{sin\alpha}{cos\alpha}}{cos\alpha+\dfrac{cos\alpha}{sin\alpha}}\)\(=\dfrac{sin\alpha cos\alpha+sin\alpha}{cos\alpha}:\dfrac{cos\alpha sin\alpha+cos\alpha}{sin\alpha}\)
\(=\dfrac{sin\alpha cos\alpha+sin\alpha}{cos\alpha}.\dfrac{sin\alpha}{cos\alpha sin\alpha+cos\alpha}\)
\(=\dfrac{sin^2\alpha\left(cos\alpha+1\right)}{cos^2\alpha\left(sin\alpha+1\right)}>0\) nếu biểu thức có nghĩa.
4 tháng 8 2018
a) ta có : \(A=\left(sin\alpha+cos\alpha\right)^2+\left(sin\alpha-cos\alpha\right)^2\)
\(\Leftrightarrow A=sin^2\alpha+2sin\alpha.cos\alpha+cos^2\alpha+sin^2\alpha-2sin\alpha.cos\alpha+cos^2\alpha\)
\(\Leftrightarrow A=2\left(sin^2\alpha+cos^2\alpha\right)=2.1=2\) (không phụ thuộc vào \(\alpha\))
\(\Rightarrow\left(đpcm\right)\)
\(B=sin^6\alpha+cos^6\alpha+3sin^2\alpha.cos^2\alpha\)
\(\Leftrightarrow B=\left(sin^2\alpha+cos^2\alpha\right)^3-3sin^2\alpha.cos^2\alpha\left(sin^2\alpha+cos^2\alpha\right)+3sin^2\alpha.cos^2\alpha\)
\(\Leftrightarrow B=\left(sin^2\alpha+cos^2\alpha\right)^3-3sin^2\alpha.cos^2\alpha+3sin^2\alpha.cos^2\alpha\)
\(\Leftrightarrow B=\left(sin^2\alpha+cos^2\alpha\right)^3=1^3=1\) (không phụ thuộc vào \(\alpha\) ) \(\Rightarrow\left(đpcm\right)\)
4 tháng 8 2018
a/A = sin2 + 2. sin.cos + cos2 + sin2 -2cos.sin + cos2= 2
Tớ không biết ghi anpha nên .. 
NL
0
TC
1
TT
22 tháng 4 2018
Mình viết luôn là sin với cos, bạn tự cho thêm \(\alpha\) nhé.
VT= \(\sin^2.\dfrac{\sin}{\cos}+\cos^2.\dfrac{\cos}{\sin}+2\sin\cos\)
= \(\dfrac{\sin^3}{\cos}+\dfrac{\cos^3}{\sin}+2\sin\cos\)
= \(\dfrac{\sin^4+\cos^4+2\sin^2.\cos^2}{\cos.\sin}\)
= \(\dfrac{\left(\sin^2+\cos^2\right)^2}{\cos.\sin}\)
= \(\dfrac{1}{\sin.\cos}\)(1)
VP = \(\dfrac{\sin}{\cos}+\dfrac{\cos}{\sin}\)
= \(\dfrac{\sin^2+\cos^2}{\cos.\sin}\)
= \(\dfrac{1}{\cos.\sin}\)(2)
từ (1) và (2) => VT=VP (đpcm)
Chúc bạn học tốt!