Tìm giá trị nhỏ nhất của m sao cho \(y=\frac{1}{3}x^3+mx^2-mx-m\)đồng biến trên R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 1 2017
Hàm số đồng biến trên R
⇔ y ' = x 2 + 2 m x - m ≥ 0 ⇔ ∆ ' = m 2 + m ≤ 0 ⇔ - 1 ≤ m ≤ 0
Suy ra giá trị nhỏ nhất của m là -1
Đáp án B
TL
1
8 tháng 9 2023
\(y'=\dfrac{1}{3}\cdot3x^2-m\cdot2x+2m+3=x^2-2m\cdot x+2m+3\)
Để hàm số đồng biến trên R thì y'>=0 với mọi x thuộc R
=>Δ=(-2m)^2-4(2m+3)<=0 và 1>0
=>4m^2-8m-12<=0
=>m^2-2m-3<=0
=>(m-3)(m+1)<=0
=>-1<=m<=3
mà m nguyên
nên \(m\in\left\{-1;0;1;2;3\right\}\)
11 tháng 11 2023
a: \(y=-\dfrac{1}{3}x^3-mx^2+4x+2021m\)
=>\(y'=-\dfrac{1}{3}\cdot3x^2-m\cdot2x+4\)
=>\(y'=-x^2-2m\cdot x+4\)
Để hàm số nghịch biến trên R thì \(y'< =0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(-2m\right)^2-4\cdot\left(-1\right)\cdot4< =0\\-1< 0\end{matrix}\right.\)
=>\(4m^2+16< =0\)
mà \(4m^2+16>=16>0\forall m\)
nên \(m\in\varnothing\)
b: \(y=-\dfrac{1}{3}\cdot x^3-\dfrac{1}{2}\cdot m\cdot x^2+x+20\)
=>\(y'=-\dfrac{1}{3}\cdot3x^2-\dfrac{1}{2}\cdot m\cdot2x+1\)
=>\(y'=-x^2-m\cdot x+1\)
Để hàm số nghịch biến trên R thì \(y'< =0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(-m\right)^2-4\cdot\left(-1\right)\cdot1< =0\\-1< 0\end{matrix}\right.\)
=>\(m^2+4< =0\)
mà \(m^2+4>=4>0\forall m\)
nên \(m\in\varnothing\)
12 tháng 11 2023
a: \(y=-x^3-3x^2+\left(5-m\right)x\)
=>\(y'=-3x^2-3\cdot2x+5-m\)
=>\(y'=-3x^2-6x+5-m\)
Để hàm số nghịch biến trên R thì \(y'< =0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(-6\right)^2-4\cdot\left(-3\right)\left(5-m\right)< =0\\-3< 0\end{matrix}\right.\)
=>\(36+12\left(5-m\right)< =0\)
=>\(36+60-12m< =0\)
=>\(-12m+96< =0\)
=>-12m<=-96
=>m>=8
b: \(y=x^3+\left(2m-2\right)\cdot x^2+mx\)
=>\(y'=3x^2+2\left(2m-2\right)\cdot x+m\)
=>\(y'=3x^2+\left(4m-4\right)x+m\)
Để hàm số đồng biến trên R thì y'>=0 với mọi x
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3>0\\\left(4m-4\right)^2-4\cdot3\cdot m< =0\end{matrix}\right.\)
=>\(16m^2-32m+16-12m< =0\)
=>\(16m^2-44m+16< =0\)
=>\(4m^2-11m+4< =0\)
=>\(\dfrac{11-\sqrt{57}}{8}< =m< =\dfrac{11+\sqrt{57}}{8}\)
27 tháng 10 2021
a: để hàm số đồng biến trên R thì m-1>0
hay m>1
b: Để hàm số nghịch biến thì m>0
12 tháng 11 2023
a: ĐKXĐ: x<>m
=>TXĐ: D=R\{m}
\(y=\dfrac{mx-2m-3}{x-m}\)
=>\(y'=\dfrac{\left(mx-2m-3\right)'\cdot\left(x-m\right)-\left(mx-2m-3\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{m\left(x-m\right)-\left(mx-2m-3\right)}{\left(x-m\right)^2}\)
\(=\dfrac{mx-m^2-mx+2m+3}{\left(x-m\right)^2}=\dfrac{-m^2+2m+3}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\in TXĐ\)
=>\(\dfrac{-m^2+2m+3}{\left(x-m\right)^2}>0\)
=>\(-m^2+2m+3>0\)
=>\(m^2-2m-3< 0\)
=>(m-3)(m+1)<0
TH1: \(\left\{{}\begin{matrix}m-3>0\\m+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>3\\m< -1\end{matrix}\right.\)
=>\(m\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}m-3< 0\\m+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-1\\m< 3\end{matrix}\right.\)
=>-1<m<3
b: TXĐ: D=R\{m}
\(y=\dfrac{mx-4}{x-m}\)
=>\(y'=\dfrac{\left(mx-4\right)'\left(x-m\right)-\left(mx-4\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{m\left(x-m\right)-\left(mx-4\right)}{\left(x-m\right)^2}\)
\(=\dfrac{mx-m^2-mx+4}{\left(x-m\right)^2}=\dfrac{-m^2+4}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(\dfrac{-m^2+4}{\left(x-m\right)^2}>0\)
=>\(-m^2+4>0\)
=>\(-m^2>-4\)
=>\(m^2< 4\)
=>-2<m<2
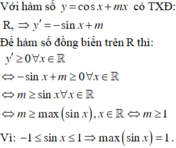
\(-1\le m\le0\)