cho tam giác ABC có AB=16, AC=14, góc B=600. Tính BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


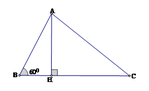
Kẻ đường cao AH
Xét tam giác vuông ABH, ta có:
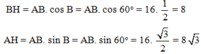
Áp dụng định lý Py-ta-go vào tam giác vuông AHC ta có:
![]()
Suy ra HC = 2.
Vậy BC = CH + HB = 2 + 8 = 10
Đáp án cần chọn là: A


a: Xét ΔABC có \(AB^2=AC^2+BC^2\)
nên ΔABC vuông tại C



3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)

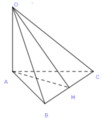
Gọi H là chân đường cao kẻ từ A xuống BC trong tam giác ABC.
+ Ta có: A H ⊥ B C O A ⊥ B C ⇒ B C ⊥ O A H ⇒ O H ⊥ B C ⇒ d(O; BC) = OH
+ Nửa chu vi tam giác ABC: p = 14 + 16 + 10 2 = 20
S A B C = 20 20 − 14 20 − 16 20 − 10 = 40 3 (theo công thức Hê-rông)
Lại có S A B C = 1/2AH.BC ⇒ AH = 2 S A B C B C = 80 3 10 = 8 3 .
+ Tam giác OAH vuông tại A (OA ⊥ AH)
⇒ OH = O A 2 + A H 2 = 8 2 + 8 3 2 = 16.
Vậy d(O; BC) = OH = 16.
Đáp án B
Ta có: AC2 = AB2 + BC2 - 2AB.BC.cos(ABC)
<=> 142 = 162 + BC2 -2.16.BC.cos(60)
<=> BC2 - 16BC + 60 = 0
<=> BC = 6 hoặc BC = 10
Thoe bất đẳng thức tam giác thì car2 trường hợp trên đều thỏa mãn
Vậy BC = 6 hoặc BC = 10