Cho điểm M cố định trên đoạn thẳng AB. Vẽ về 1 phía với AB : Ax và By cùng vuông góc với AB. Qua M có 2 đường thẳng thay đổi luôn luôn vuông góc với nhau và cắt Ax, By tại C và D.a) C/m : ΔACM đồng dạng ΔBMD.b) Cho \(\widehat{AMC}=\alpha;AM=a;BM=b.\) Tính diện tích ΔCMD theo α;a;bc) Xác định vị trí của C và D để...
Đọc tiếp
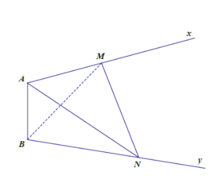
Cho điểm M cố định trên đoạn thẳng AB. Vẽ về 1 phía với AB : Ax và By cùng vuông góc với AB. Qua M có 2 đường thẳng thay đổi luôn luôn vuông góc với nhau và cắt Ax, By tại C và D.
a) C/m : ΔACM đồng dạng ΔBMD.
b) Cho \(\widehat{AMC}=\alpha;AM=a;BM=b.\) Tính diện tích ΔCMD theo α;a;b
c) Xác định vị trí của C và D để SΔMCD có GTNN.
<br class="Apple-interchange-newline"><div></div>ΔACM∼ΔBMD(g−g)⇒ACMB =AMBD
⇒AC.BD=AM.MB=const⇒xy=c=const
SMCD=SACDB−SACM−SMBD=(x+y)(AM+MB)2 −x.AM2 −y.MB2
=x.MB+y.AM2 ≥√xy.MB.AM=√c2=c
Dấu bằng xảy ra khi x.MB = y.AM, lại có xy=MB.AM⇒{
Vậy giá trị nhỏ nhất của S CMD=c(đvdt) xảy ra khi AC = AM; BD = BM.
Xl nha lúc copy thì gặp sự cố