Cho hình thang vuông ABCD (AB//CD) có : A=D=90 , AB=5cm,AD=12cm,BC=13cm. Tính CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 7 2019
1, Ta có AB // CD
\(\Rightarrow\widehat{A}+\widehat{D}=180^0\)( 2 GÓC TRONG CÙNG PHÍA )
ta lại có \(\widehat{A}-\widehat{D}\)= 400
cộng vế vs vế ta đc \(2\widehat{A}=220^0\)
\(\widehat{A}=110^0\) \(\Rightarrow\widehat{D}=70^0\)
ta có \(\widehat{A}=2\widehat{C}\Rightarrow\widehat{C}=55^0\)
ta có \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)(tổng 4 góc trong tứ giác)
\(\Rightarrow\widehat{B}=125^0\)
#mã mã#
CC
12 tháng 9 2018
Xét tam giác ABC vuông tại A
=>\(AB^2\)+\(AD^2\)=\(BD^2\)
=>BD=13(theo định lí pi ta go)
=>BD=BC=tam giác BDC cân tại B
Kẻ đường cao BI
=>BI là đường trung tuyến tam giác BID vuông tại I
=>tam giác=tam giác(cạnh huyền góc nhọn)(tử tìm nha)
Xét tam giác BID vuông tại I có:
\(BD^2\)=\(BI^2\)+\(BI^2\)(theo định lí pi ta go)
=>ID=IC=\(13^2\)-\(12^2\)=25=5
=>ID+IC=DC=5.2=10
-----------------------------------học tốt ko cần mik đâu---------------------
1 tháng 7 2018
Ta áp dụng công thức Brahmagupta để tính
\(s=\frac{\sqrt{\left(AB^2+CD^2+BD^2+AC^2\right)+8\cdot AB\cdot CD\cdot BD\cdot AC-2\left(AB^4+CD^4+BD^4+AC^4\right)}}{4}\)
A) Thay số vào ta đc \(S=6\sqrt{55}\approx44,4972\left(cm^2\right)\)
b) \(S\approx244,1639\left(cm^2\right)\)
hok tốt ...
CN
26 tháng 7 2019
Công thức Brahmagupta là công thức tính diện tích của một tứ giác nội tiếp (tứ giác mà có thể vẽ một đường tròn đi qua bốn đỉnh của nó) mà hình thang ko có đường tròn nào đi qua đủ bốn đỉnh của nó nên công thức này ko được áp dụng vào bài này
CM
30 tháng 10 2018
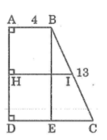
Kẻ BE ⊥ CD
Suy ra tứ giác ABED là hình chữ nhật
Ta có: AD = BE
AB = DE = 4 (cm)
Suy ra: CE = CD – DE = 9 – 4 = 5 (cm)
Áp dụng định lí Pitago vào tam giác vuông BCE ta có :
B C 2 = B E 2 + C E 2
Suy ra : B E 2 = B C 2 - C E 2 = 13 2 - 5 2 = 144
BE = 12 (cm)
Vậy: AD = 12 (cm)
BT
3
4 tháng 7 2015
Từ B kẻ BH _|_DC. Ta có HC=DC-AB=5.
Từ đó tính được BH = \(\sqrt{13^2-5^2}=12\)
Vậy AD=12cm
TB
3
NT
0
Xét \(\Delta\)ABD vuông tại A
Áp dụng định lí Py-ta-go, ta có:
BD2 = AD2 + AB2
\(\Rightarrow\) BD2 = 122 + 52 = 169 (cm)
\(\Rightarrow\) BD = \(\sqrt{169}\) = 13 (cm) Xét \(\Delta\) BCD có BC = BD = 13 cm \(\Rightarrow\) \(\Delta\) BCD cân tại B Qua B kẻ đường cao BH cắt CD tại H \(\Rightarrow\) BH cũng là đường trung tuyến ( vì \(\Delta\) BCD cân tại B ) Xét tứ giác ABHD có \(\widehat{BAD}=\widehat{ADH}=\widehat{BHD}=90\)0 \(\Rightarrow\) tứ giác ABHD là HCN \(\Rightarrow\) HB = AD = 12 cm Xét \(\Delta\) BHC có \(\widehat{BHC}=90\)0 Áp dụng định lí Py-ta-go, ta có: BC2 = HB2 + HC2 \(\Rightarrow\) 132 = 122 + HC2 \(\Rightarrow\) HC2 = 132 - 122 = 25 ( cm) \(\Rightarrow\) HC = \(\sqrt{25}=5\left(cm\right)\) Vì BH cũng là đường trung tuyến (cmt) \(\Rightarrow\) CD = 2*5 = 10 (cm) \(\Rightarrow\) đpcm