Hai lò xo có cùng chiều dài tự nhiên. Khi treo vật m= 200g bằng lò xo k1 thì nó dao động với chu kì T1=0,3s. Thay bằng lò xo k2 thì chu kì là T2=0,4s. Mắc hai lò xo nối tiếp và muốn chu kì mới bây giờ là trung bình cộng của T1 và T2 thì phải treo vao phía dưới một vật khối lượng m' bằng bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

23 tháng 9 2021
tỉ lệ T1/T2=4/3=> k1/k2= 9/16=> song song k=k1+k1=9/16+1=25/16=> T ss/T2=4/5=0,48s

VT
15 tháng 6 2018
Chọn B
+ Có 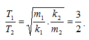
Thay m1 = 4m2 => ![]()
+ Mắc hai lò xo k1, k2 thành một lò xo dài gấp đôi, đầu trên cố định, đầu dưới treo vật m2.
=> Độ cứng của lò xo mới là:
![]()
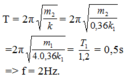

1 tháng 7 2016
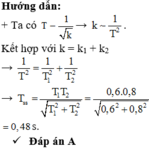
Chu kì: \(T=2\pi\sqrt{\dfrac{m}{k}}\)
\(\Rightarrow T^2\) tỉ lệ với \(\dfrac{1}{k}\), ta đặt \(T^2=\dfrac{a}{k}\)
Lò xo l1 thì: \(T_1^2=\dfrac{a}{k_1}\) (1)
Lò xo l2 thì: \(T_2^2=\dfrac{a}{k_2}\) (2)
Theo đề bài ta có 2 lò xo mắc song song: \(k=k_1+k_2\)
\(T^2=\dfrac{a}{k}\) (3)
Từ (1), (2) và (3) ta suy ra: \(\dfrac{1}{T^2}=\dfrac{1}{T_1^2}+\dfrac{1}{T_2^2}\)
Đến đây bạn tính tiếp nhé.




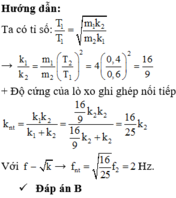
\(T_1=2\pi\sqrt{\dfrac{m}{k_1}}\Rightarrow \dfrac{1}{k_1}=\frac{{T_1}^{2}}{{(2\pi)}^{2}m}\)
\(T_2=2\pi\sqrt{\dfrac{m}{k_2}}\Rightarrow \frac{1}{k_2}=\frac{{T_2}^{2}}{{(2\pi)}^{2}m}\)
Mắc nối tiếp 2 lò xo thì ta có: \(\dfrac{1}{k}=\dfrac{1}{k_1}+\dfrac{1}{k_2}=\frac{{T_1}^{2}}{{(2\pi)}^{2}m}+\frac{{T_2}^{2}}{{(2\pi)}^{2}m}=\frac{1}{{(2\pi)}^{2}m}(T_1^2+T_2^2)\)
Thay vào biểu thức
\(T=2\pi\sqrt{\dfrac{m'}{k}} =\sqrt{\dfrac{m'}{m}.(T_1^2+T_2^2)}\)
\(\Rightarrow \dfrac{0,3+0,4}{2}=0,5.\sqrt{\dfrac{m'}{m}}\)
\(\Rightarrow \dfrac{m'}{m}=0,49\)
\( \Rightarrow m'=0,49.m=0,49.200=98g \)