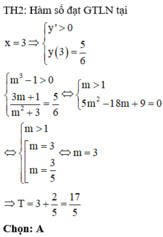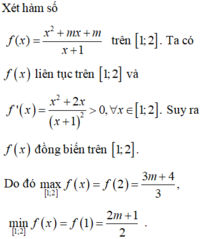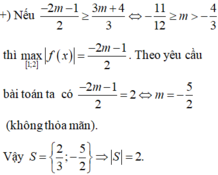tìm tổng tất cra các giá trị của tham số thực m để hàm số y=|mx-1|-x^2 có giá trị lớn nhất bằng 10/8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.

+ Đạo hàm f'(x) = 2 - m x 2 ( x + 1 ) x ( x + 1 )
f'(x) = 0 ⇒ x = 2 m ↔ x = m 2 4 ∈ [ 0 ; 4 ] , ∀ m > 1
+ Lập bảng biến thiên, ta kết luận được
m a x [ 0 ; 4 ] f ( x ) = f ( 4 m 2 ) = m 2 + 4
+ Vậy ta cần có m 2 + 4 < 3
↔ m < 5 → m > 1 m ∈ ( 1 ; 5 )
Chọn C.

Đáp án A
Phương pháp giải:
Xét các trường hợp của tham số, lập bảng biến thiên để tìm max – min trên đoạn
Lời giải:
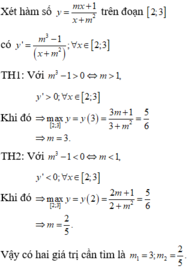

Chọn B
Nếu m = 1 thì y = 1 (không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8)
Nếu m
≠
1 thì hàm số đã cho liên tục trên [1;2] và 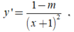
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn [1;2]
Do vậy ![]()
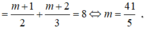


Vì hàm số đã cho là hàm bậc nhất trên bậc nhất nên hàm số đơn điệu trên từng khoảng xác định của hàm số.
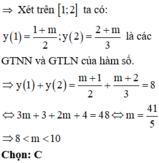


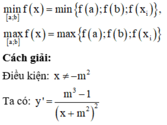
Hàm số bậc nhất trên bậc nhất luôn đồng biến hoặc nghịch biến trên từng khoảng xác định của nó.