Người ta trồng 3003 cây theo hình tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ hai có 2 cây, hàng thứ 3 có 3 cây,v.v....Hỏi có bao nhiêu hàng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
13 tháng 2 2018
Chọn C.
Số cây mỗi hàng (bắt đầu từ hàng thứ nhất) lập thành một cấp số cộng có u1 = 1; d = 1
Giả sử có n hàng cây thì
Ta có 3003 = Sn = nu1 + ![]() ⇔ n2 + n – 6006 = 0 ⇔ n = 77.
⇔ n2 + n – 6006 = 0 ⇔ n = 77.

CM
27 tháng 8 2019
Chọn B.
Gọi số hàng cây là n.
Gọi số cây lần lượt trên các hàng là 1; 2; 3..; n.
Đây là một cấp số cộng với số hạng đầu u1 = 1; d = 1 .
Ta có:
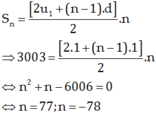
Vậy số hàng cần tìm là 77.

CM
28 tháng 11 2017
Đáp án C.
Phương pháp: Sử dụng tổng 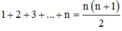
Cách giải: Giả sử trồng được n hàng cây với quy luật trên thì số cây trồng được là:
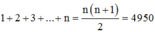
![]()
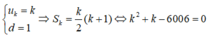
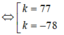

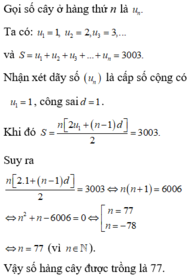


Theo giả thiết: 1+2+3+...+n=3003
⇔n(n+1)2=3003
⇔n2+n−6006=0
⇔[n=−78(L)n=77(TM)
Vậy có 77 hàng cây.
Ta gọi số hàng cây là: n
Thì ta có số cây sẽ là: 1 + 2 + 3 +...... n-1 + n = n(n+1)/2 (công thức n(n+1) hình như đã học rồi và đã đc chứng minh)
Nếu theo bạn nói thì ta sẽ có một công thức sau: n(n+1)/2 = 3003
<=> n² + n - 6006 = 0
=> n= 77 hoặc n= -78
Vậy ta chọn số hàng cây là 77