Một hệ được bố trí như sau: lò xo có độ cứng \(k\), đặt thẳng đứng, đầu dưới gắn vào sàn, đầu trên gắn cố định vào vật có khối lượng \(m_1\). Đặt vật có khối lượng \(m_2\)lên trên \(m_1\) (không gắn chặt hai vật với nhau). Cho hệ dao động. Để \(m_2\) luôn nằm trên \(m_1\) thì điều kiện của biên độ dao động là gì?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cơ năng \(W=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2\)
Vật nằm ngang v = 0 => \(W=\dfrac{1}{2}kx^2=\dfrac{1}{2}\cdot200\cdot0,05^2=0,25\left(J\right)\)
Đáp án : A) 25.10^-2
B. 50.10^-2
C. 100.10^-2
D. 200.10^-2
Vậy đáp án A ạ?

Động năng:
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,1\cdot0^2=0J\)
Thế năng đàn hồi:
\(W_{đh}=\dfrac{1}{2}k\left(\Delta x\right)^2=\dfrac{1}{2}\cdot200\cdot0,05^2=0,25J\)
Cơ năng hệ:
\(W=W_đ+W_{đh}=0+0,25=0,25J\)

Ta có: K = 25 N/m; Δl = 4 cm = 0,04 m.
Khi cân bằng ta có
\(\begin{array}{l}P = {F_{dh}} \Leftrightarrow mg = K.\left| {\Delta l} \right|\\ \Rightarrow m = \frac{{K.\left| {\Delta l} \right|}}{g} = \frac{{25.0,04}}{{9,8}} \approx 0,1(kg)\end{array}\)

Đáp án C
+ Độ biến dạng của lò xo tại vị trí cân bằng ∆ l 0 = m g k = 2 , 5 c m
+ Từ vị trí cân bằng, ấn vật xuống dưới 2,5 cm rồi buông nhẹ -> vật sẽ dao động với biên độ A=2,5 cm
Lực đàn hồi lớn nhất tác dụng lên giá đỡ khi vật ở biên dưới F m a x = k ∆ l 0 + A = 3 , 2 N
Lực đàn hồi nhỏ nhất tác dụng lên giá đỡ khi vật ở vị trí biên trên, tại vị trí này lò xo không biến dạng → F m i n = 0
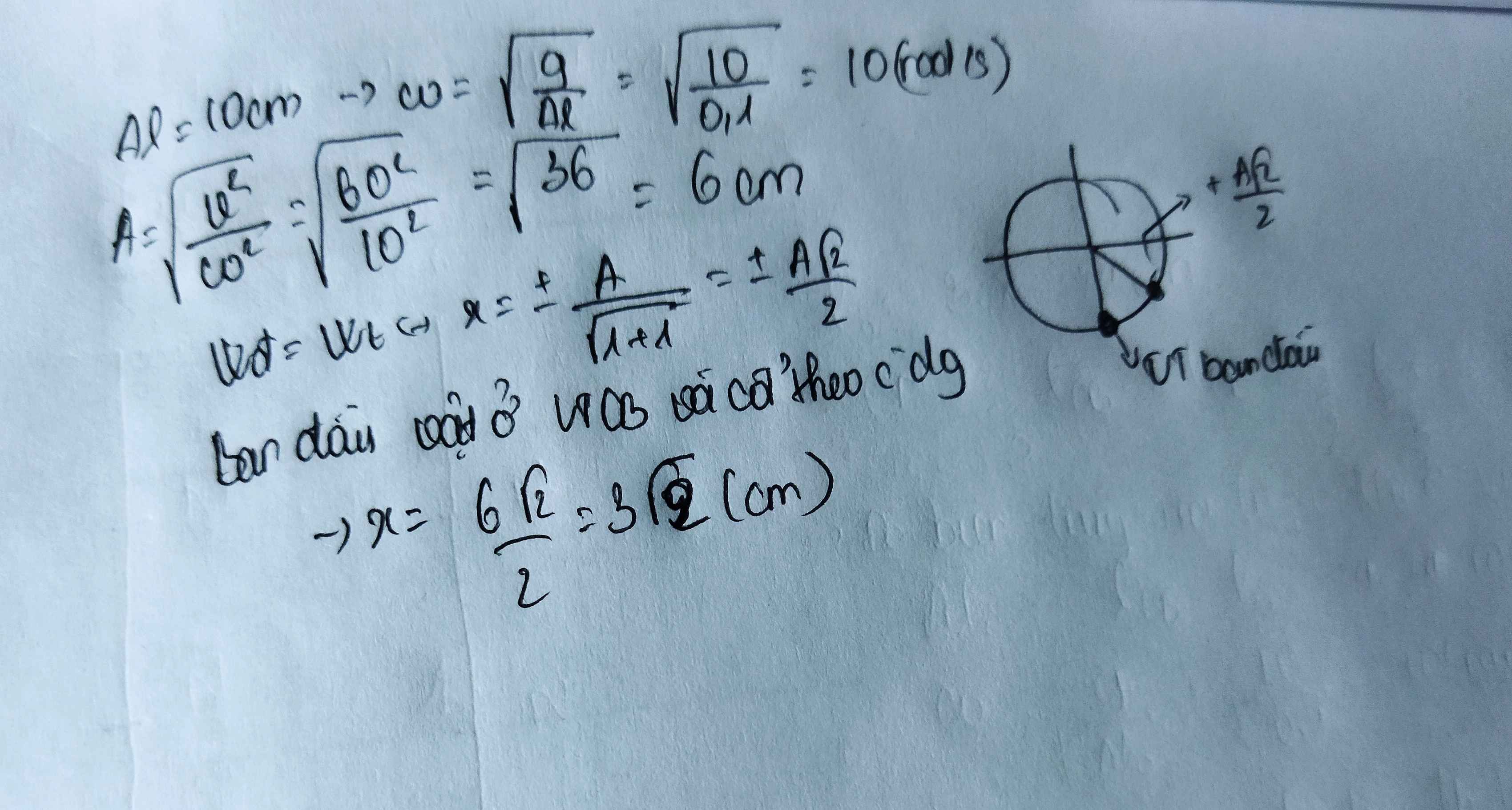

Với biên độ thỏa mãn để vật 2 luôn nằm trên vật 1 thì
\(\omega=\sqrt{\frac{k}{m_1+m_2}}\) Gia tốc lớn nhất trong quá trì chuyển động là khi các vật ở vị trí biên \(\left|a\right|=A\omega^2\) Xét hệ quy chiếu gắn với vật 1 thì vật 2 chịu các lực là trọng lực của nó, lực quán tính, và phản lực từ vật 1 Vật sẽ rời khi phản lực bằng 0, khi đó các vật ở vị trí cao nhất gia tốc a hướng xuống nên lực quán tính hướng lên \(m_2a=m_2g\) \(A\omega^2=g\) \(A=\frac{g}{\omega^2}=\frac{g\left(m_1+m_2\right)}{k}\)