Điện năng được truyền từ nơi phát đến một khu dân cư bằng đường dây một pha với hiệu suất truyền tải là 90%. Coi hao phí điện năng chỉ do tỏa nhiệt trên đường dây và không vượt quá 20%. Nếu công suất sử dụng điện của khu dân cư này tăng 20% và giữ nguyên điện áp ở nơi phát thì hiệu suất truyền tải điện năng trên chính đường dây đó là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
26 tháng 5 2019
Đáp án D
+ Phương trình truyền tải điện năng trong hai trường hợp: 
Với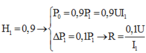 
+ Thay vào phương trình truyền tải thứ hai (lưu ý rằng điện áp nơi truyền đi là như nhau) ta thu được phương trình:
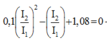Phương trình cho ta hai nghiệm
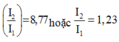
→ Hiệu suất truyền tải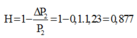 
VT
7 tháng 8 2018
Đáp án: A
- Ban đầu ta có: P 1 = ∆ P + P 2 mà H 1 = 0 , 9 → P 2 = 0 , 9 P 1 = 0 , 9 U I 1 ∆ P 1 = 0 , 1 P 1 → R = 0 , 1 U I 1 (1)
- Sau đó P 1 ' = ∆ P ' + P 2 ' ⇔ U I 2 = R I 2 2 + 1 , 1 P 2 (2)
- Từ (1) và (2) ta có: U I 2 = 0 , 1 U I 2 2 I 1 + 1 , 1 . 0 , 9 U I 1 ⇔ 0 , 1 I 2 I 1 2 - I 2 I 1 + 1 , 1 . 0 , 9 = 0 (3)
- Giải phương trình (3) ta có hai nghiệm: I 2 I 1 = 1 , 114 I 2 I 1 = 8 , 886
- Hiệu suất truyền tải H = P 2 ' P 1 ' = 1 - ∆ P 2 ' P 1 ' = 1 - R I 2 2 U I 2 ⇔ H = 1 - 0 , 1 I 2 I 1 (4)
- Vì hao phí không vượt quá 20% nên ta chọn nghiệm I 2 I 1 = 1,114.
Thay vào (4) ta có H = 88,86%
VT
8 tháng 8 2019
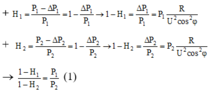
+ P1 = P0 + DP1 và P2 = 1,2P0 + DP2 → H1P1 = P1 - DP1 = P0
Và H2P2 = (P2 - DP2) = 1,2P0 → 1,2H1P1 = H2P2
VT
6 tháng 11 2018
Chọn A
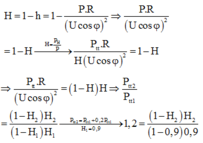
+ H 1 = P 1 - ∆ P 1 P 1 = 1 - ∆ P 1 P 1 → 1 - H 1 = ∆ P 1 P 1 = P 1 R U 2 cos 2 φ
+ H 2 = P 2 - ∆ P 2 P 2 = 1 - ∆ P 2 P 2 → 1 - H 2 = ∆ P 2 P 2 = P 2 R U 2 cos 2 φ
® 1 - H 1 1 - H 2 = P 1 P 2 (1)
+ P 1 = P 0 + D P 1 và P 2 = 1,2 P 0 + D P 2 ® H 1 P 1 = P 1 - D P 1 = P 0
Và H 2 P 2 = ( P 2 - D P 2 ) = 1,2 P 0 ® 1,2 H 1 P 1 = H 2 P 2 → P 1 P 2 = H 2 1 , 2 H 1 2
+ Từ (1) và (2) ta được: 1 - H 1 1 - H 2 = H 2 1 , 2 H 1 → H 2 2 - H 2 + 0 , 108 = 0
® H 2 = 0,1232 = 12,32 % < 20% (loại) và H 2 = 0,877 = 87,7%
VT
10 tháng 6 2017
Phương pháp: Công suất hao phí trên đường dây
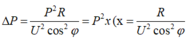
(không đổi)
Cách giải: Ban đầu:
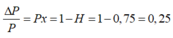
Sau khi công suất sử dụng tăng lên 25%:
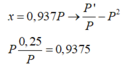
Đặt P’/P = m, ta có:
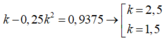
Với k = 2,5
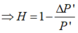
(loại vì hao phí không quá 40%)
Với k = 1,5
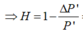
=>Chọn C
(loại vì hao phí không quá 40%)
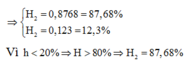
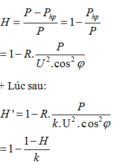
Công suất hao phí trên đường dây \(\Delta p=\frac{P^2R}{U^2\cos^2\varphi}=P^2X\) \(\left(X=\frac{R}{U^2\cos^2\varphi}\text{ không đổi}\right)\)
Ban đầu: \(\frac{\Delta P_1}{P_1}=P_1X=0,1\)
Sau khi công suất sử dụng tăng lên 20% ta có :
\(P_2-\Delta P_2=1,2\left(P_1-\Delta P_1\right)=1,08P_1\)
\(\Rightarrow P_2-P_2^2X=1,08P_1\)
\(\Rightarrow\frac{P_2}{P_1}-\frac{P_2^2.0,1}{P_1^2}=1,08\)
Đặt \(\frac{P_2}{P_1}=k\) :
\(\Rightarrow0,1k^2-k+1,08=0\)
\(\Rightarrow\begin{cases}k=8,77\\k=1,23\end{cases}\)
Nếu k = 8,77 thì: \(H=1-\frac{\Delta P_2}{P_2}=1-P_2X=1-8,77P_1X=0,123=12,3\%\) (loại, vì hao phí không quá 20%)
Nếu k = 1,23 thì: \(H=1-\frac{P_2^2}{P_2}=1-P_2X=1-1,23P_1X=0,877=87,7\%\)
Vậy chọn C. 87,7%
hay