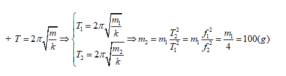Một lò xo có độ cứng 100N/m, lần lượt treo hai quả nặng khối lượng m1, m2 vào lò xo và kích thích cho chúng dao động thì thấy: trong cùng một khoảng thời gian, m1 thực hiện được 3 dao động, m2 thực hi...

E

erosennin

29 tháng 7 2021

Một lò xo có độ cứng 100N/m, lần lượt treo hai quả nặng khối lượng m1, m2 vào lò xo và kích thích cho chúng dao động thì thấy: trong cùng một khoảng thời gian, m1 thực hiện được 3 dao động, m2 thực hiện được 9 dao động. Nếu treo cả hai quả cầu vào lò xo thì chu kỳ dao động của hệ là 0,2π (s). Giá trị của...

Đọc tiếp

#Vật lý lớp 12

1

HT

Hoàng Tử Hà

29 tháng 7 2021

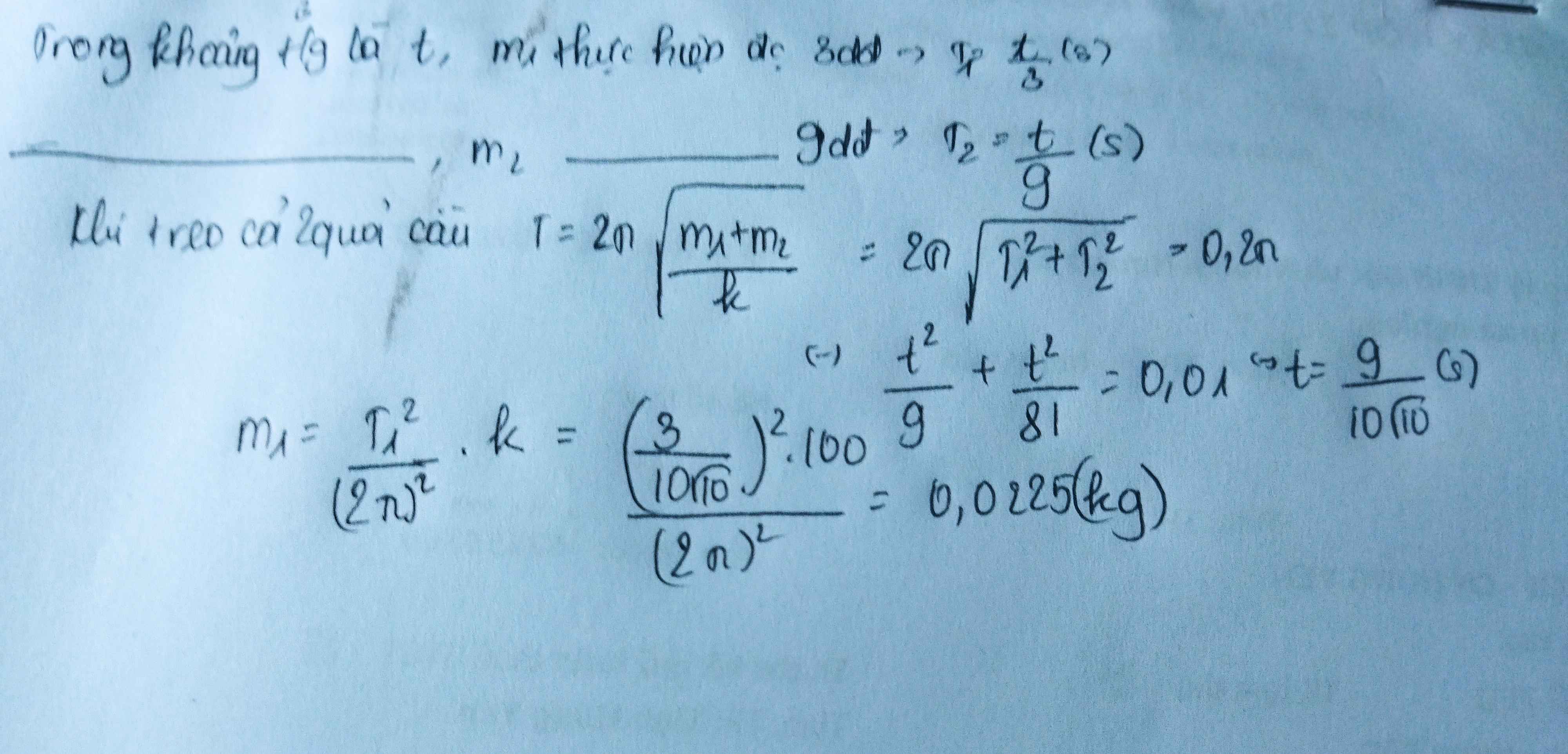
undefined

Đúng(1)

HD

Hoàng Đức Long

29 tháng 7 2019

Một lò xo có độ cứng 96N/m, lần lượt treo hai quả cầu khối lượng m 1 , m 2 vào lò xo và kích thích cho chúng dao động thì thấy: trong cùng một khoảng thời gian m 1 thực hiện được 10 dao động, m 2 thực hiện được 5 dao động. Nếu treo cả 2 quả cầu vào lò xo thì chu kỳ dao động của hệ là π 2 (s). Giá trị của là...

Đọc tiếp

#Vật lý lớp 12

1

VT

Vũ Thành Nam

29 tháng 7 2019

Đúng(0)

LP

Lê Phương Thảo

14 tháng 8 2021

Câu 1. Một lò xo có độ cứng k = 25 N/m. Lần lượt treo hai quả cầu có khối lượng m1, m2 vào lò xo và kích thích cho dao động thì thấy rằng. Trong cùng một khoảng thời gian: m1 thực hiện được 16 dao động, m2 thực hiện được 9 dao động. Nếu treo đồng thời 2 quả cầu vào lò xo thì chu kì dao động của chúng là T = π /5 (s). Khối lượng của hai vật lần lượt bằng ?Câu 2. Một con lắc lò xo có độ cứng k. Lần...

Đọc tiếp

#Vật lý lớp 12

0

HD

Hoàng Đức Long

19 tháng 5 2018

Lần lượt treo hai vật m1 và m2 vào một con lắc lò xo có độ cứng k = 40 N/m và kích thích dao động điều hòa. Trong cùng một khoảng thời gian nhất định m1 thực hiện 20 dao động và m2 thực hiện 10 dao động. Nếu cùng treo cả hai vật vào lò xo thì chu kỳ dao động của hệ là π/2s. Khối lượng m1 m2 lần lượt là A. 0,5kg;1,5 kg B. 0,5 kg; 2 kg C. 0,5kg;1kg D. 1kg;0,5...

Đọc tiếp

#Vật lý lớp 12

1

VT

Vũ Thành Nam

19 tháng 5 2018

Đáp án B

Phương pháp: Chu ki dao đông̣ điều hoa cua con lắc lo xo T = 2 π m k

Cách giải:

Theo bài ra ta có

Đúng(0)

TT

Tina Tina

16 tháng 7 2016

1. Hai đầu A và B của lx gắn vào hai vật nặng có khối lượng m và 3m. Hệ có thể dao động không ma sát trên mặt phẳng ngang. Khi giữ cố định điiểm C trên lò xo thì chu kì dao động hai vật bằng nhau. Tính tỉ số CB/AB khi lò xo không biến dạng?2.Một lò xo có độ cứng 96N/m, lần lượt treo hai quả cầu khối lượng m1, m2 vào lò xo và kích thích dao động thì thấy: trong cùng một khoảng thời gian m1...

Đọc tiếp

#Vật lý lớp 12

2

TH

Trần Hoàng Sơn

16 tháng 7 2016

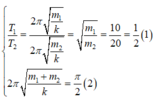
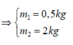
1. Chu kì 2 vật là:

\(T_1=2\pi\sqrt{\dfrac{m_1}{k_1}}\)

\(T_2=2\pi\sqrt{\dfrac{m_2}{k_2}}\)

Có \(T_1=T_2\)

\(\Rightarrow \dfrac{m_1}{k_1}=\dfrac{m_2}{k_2}\)

\(\Rightarrow \dfrac{k_2}{k_1}=\dfrac{m_2}{m_1}=3\)

Mà với 1 lò xo thì \(k.l=const\)

\(\Rightarrow k_1.l_1=k_2.l_2\)

\(\Rightarrow k_1.CA=k_2.CB\)

\(\Rightarrow \dfrac{k_2}{k_1}=\dfrac{CA}{CB}=3\)

\(\Rightarrow \dfrac{CA}{CA+CB}=\dfrac{3}{3+1}\)

\(\Rightarrow \dfrac{CA}{AB}=\dfrac{3}{4}\)

Đúng(0)

TH

Trần Hoàng Sơn

16 tháng 7 2016

Tần số dao động:

\(f_1=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m_1}}\)

\(f_2=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m_2}}\)

Ta có: \(\dfrac{f_1}{f_2}=\sqrt{\dfrac{m_2}{m_1}}=\dfrac{10}{5}=2\)

\(\Rightarrow \dfrac{m_1}{m_2}=4\)

Nếu treo cả 2 quả cầu vào lò xo thì chu kì là: \(T=2\pi\sqrt{\dfrac{m_1+m_2}{k}}=2\pi\sqrt{\dfrac{m_1+\dfrac{m_1}{4}}{96}}=\dfrac{\pi}{2}\)

\(\Rightarrow m_1 = 4,8kg\)

Đúng(0)

E

erosennin

29 tháng 7 2021

Gắn lần lượt hai quả cầu có khối lượng m₁ và m₂ vào một lò xo và cho chúng dao động. Trong cùng một khoảng thời gian, quả cầu m₁ thực hiện 10 dao động còn quả cầu m₂ thực hiện được 5 dao động. So sánh m₁ và m₂?

#Vật lý lớp 12

1

HT

Hoàng Tử Hà

29 tháng 7 2021

Trong một khoảng thời gian là t, m1 thực hiện được 10 dao động=> T1=t/10 (s)

Trong một khoảng thời gian là t, m2 thực hiện được 5 dao động=> T2=t/5 (s)

Có khối lượng luôn tỉ lệ thuận với bình phương chu kỳ của vật đó => vật có chu kỳ càng lớn thì khối lượng càng lớn. Ta lại có T1<T2=> m1<m2

Đúng(1)

PH

Phạm Hoàng Phương

22 tháng 8 2015

Lần lượt treo vật m1, m2 vào 1 CLLX có k=40N/m và kích thích chúng dao động trong khoảng thời gian nhất định, m1 thực hiện được 20 dao động, m2 thực hiện được 10 dao động. Nếu cùng treo cả hai vật đó vào lò xo thì chu kỳ dao động của hệ là \(\frac{\pi}{2}\). tìm m1, m2 ?

#Vật lý lớp 12

1

HD

Hà Đức Thọ

Admin

24 tháng 8 2015

Ta có: \(t=20T_1=10T_2\Rightarrow\frac{T_1}{T_2}=\frac{1}{2}\)

\(\Rightarrow\sqrt{\frac{m_1}{m_2}}=\frac{1}{2}\Rightarrow\frac{m_1}{m_2}=\frac{1}{4}\)(1)

Treo đồng thời 2 vật vào lò xo thì chu kì: \(T=2\pi\sqrt{\frac{m_1+m_2}{k}}=\frac{\pi}{2}\Leftrightarrow m_1+m_2=2,5\)kg (2)

Từ (1) và (2) suy ra: \(\begin{cases}m_1=0,5kg\\m_2=2kg\end{cases}\)

Đúng(0)

HD

Hoàng Đức Long

8 tháng 7 2019

Cho hai lò xo giống nhau có cùng độ cứng là k, lò xo thứ nhất treo vật m1 = 400g dao động với T1, lò xo thứ hai treo m2 dao động với chu kì T2. Trong cùng một khoảng thời gian con lắc thứ nhất thực hiện được 5 dao động, con lắc thứ hai thực hiện được 10 dao động. Khối lượng m2 bằng: A. 200g. B. 50g. C. 800g. D....

Đọc tiếp

#Vật lý lớp 12

1

VT

Vũ Thành Nam

8 tháng 7 2019

Chọn D

Đúng(0)

HD

Hoàng Đức Long

23 tháng 7 2019

Cho hai lò xo giống nhau có cùng độ cứng k, lò xo thứ nhất treo vật m 1 = 400 g dao động với chu kì T 1 , lò xo thứ hai treo vật m 2 dao động với chu kì T 2 . Trong cùng một khoảng thời gian con lắc thứ nhất thực hiện được 5 dao động, con lắc thứ hai thực hiện được 10 dao động. Khối lượng m 2 là A. 800 g B. 100 g C....

Đọc tiếp

#Mẫu giáo

1

VT

Vũ Thành Nam

23 tháng 7 2019

Đáp án B

100 g

Đúng(0)

NQ

Nguyễn Quỳnh

6 tháng 7 2021

Một lò xo có độ cứng . lần lượt treo vào lò cò hai vật có khối lượng m1,m2 kích thích cho chúng dao động,chứ kỳ tương ứng là 1s và 2s.biết khối lượng của chúng hơn kém nhau 300g.khối lượng 2 vật lần lượt bằng

#Vật lý lớp 12

1

HT

Hoàng Tử Hà

7 tháng 7 2021

\(T_1=2\pi\sqrt{\dfrac{m_1}{k}};T_2=2\pi\sqrt{\dfrac{m_2}{k}}\)

\(\dfrac{T_2}{T_1}=2\Leftrightarrow\sqrt{\dfrac{m_2}{m_1}}=2\Leftrightarrow m_2=4m_1\)

\(m_2-m_1=300\Rightarrow\left\{{}\begin{matrix}m_1=100\left(g\right)\\m_2=400\left(g\right)\end{matrix}\right.\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP