Dòng điện chạy trong đoạn mạch có biểu thức i= 2cos (\(100\pi\Gamma-\frac{\pi}{2}\)
) . Trong khoảng thời gian từ 1/200 dêdn 0,015 s cường độ . Dòng điện tức thời có giá trị bằng \(\sqrt{2}\) A VÀO những thời điểm nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
11 tháng 2 2017
Đáp án D
Từ 0 đến 0,01s = T/2 thì i = I 0 2 vào thời điểm t 1 = T 12 = 1 600 ( s ) và t 2 = 5 T 12 = 5 600 ( s )
VT
19 tháng 12 2018
Đáp án D
Từ 0 đến 0 , 01 s = T 2 thì i = I 0 2 vào thời điểm
HY
30 tháng 10 2015
Sử dụng đường tròn
Từ thời điểm 0-0.01 s thì góc quay được là \(\varphi = 0.01.\omega = \pi (rad).\)
Thời điểm t =0 ứng với điểm M; thời điểm t = 0.01s ứng với điểm N. Từ M đến N sẽ qua hai điểm P và Q có giá trị (độ lớn) 0.5I0.
tại P: \(\varphi_1 = t_1 \omega => t_1 = \frac{\pi/3}{100\pi} = \frac{1}{300}s\)
tại Q: \(\varphi_2 = t_2 \omega => t_2 = \frac{\pi/3+\pi/6+\pi/6}{100\pi} = \frac{2}{300}s\)
chọn đáp án. A
VT
5 tháng 10 2018
Đáp án C
Đoạn mạch chỉ chứa tụ thì dòng điện trong mạch sớm pha hơn điện áp một góc 0,5π → khi 
và đang tăng thì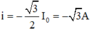 
Bạn cần tìm vị trí li độ ứng với t = 1/200 thì thay vào hàm i => i =2(VTBiên dương) ở vị trí B như hình vẽ.
Tương tự thay t = 0.015 vào i => i = -2 (VTBiên âm).C
Có 1 vị trí có giá trị \(A\sqrt{2}\) như hình vẽ
Tìm góc quay được \(\cos\varphi_1=\frac{A\sqrt{2}}{A}=\sqrt{2}\Rightarrow\varphi_1=\frac{\pi}{4}.\)
=> Thời gian quay ứng với góc phi 1 là \(t=\frac{\varphi_1}{\omega}=0.0025s.\)
Như vậy thời điểm vật ở li độ \(A\sqrt{2}\) là \(t_M=t_1+t=\frac{1}{200}+0.0025=0.0075s.\)