cho phương trình hai cạnh của một hình chữ nhật là 5x+2y-7=0. 5x+2y-36=0 và phương trình của một đường chéo là 3x+7y-10=0. viết phương trình các cạnh còn lại và đường chéo thứ hai của hình chữ nhật đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2021
Giả sử hình thoi là ABCD với \(A\left(0;1\right)\)
Do tọa độ A thỏa \(x+7y-7=0\) nên đó là cạnh chứa A, ko mất tính tổng quát, giả sử đó là cạnh AB
Tọa độ A ko thỏa pt đường chéo nên đó là đường chéo BD
\(\Rightarrow\) Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+7y-7=0\\x+2y-7=0\end{matrix}\right.\) \(\Rightarrow B\left(7;0\right)\)
Phương trình AC qua A vuông góc BD: \(2\left(x-0\right)-1\left(y-1\right)=0\Leftrightarrow2x-y+1=0\)
Tọa độ tâm I là nghiệm: \(\left\{{}\begin{matrix}x+2y-7=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow I\left(1;3\right)\)
I là trung điểm AC \(\Rightarrow C\left(2;5\right)\)
I là trung điểm BD \(\Rightarrow D\left(-5;-3\right)\)
Biết tọa độ các đỉnh, bạn tự viết pt các cạnh nhé
8 tháng 5 2016
Từ giả thiết suy ra điểm A không nằm trên 2 cạnh có phương trình đã cho. Bởi vậy, đó là phương trình của 2 đường thẳng chứa cạnh BC, CD, chẳng hạn \(BC:2x-3y+5\)
\(CD:3x+2y-7=0\)
Khi đó, đường thẳng chứa cạnh AB đi qua \(A\left(2;-3\right)\) và song song với đường thẳng CD, nên có phương trình :
\(3\left(x-2\right)+2\left(y+3\right)=0\)
hay : \(3x+2y=0\) ẳng chứa cạnh AD là :
\(2x-3y-11=0\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 1 2022
B là giao điểm của BD và AB nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+2y-7=0\\x+7y-7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=7\\y=0\end{matrix}\right.\) \(\Rightarrow B\left(7;0\right)\)
Đường chéo AC qua A và vuông góc BD nên nhận (2;-1) là 1 vtpt
Phương trình AC:
\(2\left(x-0\right)-1\left(y-1\right)=0\Leftrightarrow2x-y+1=0\)
Gọi I là giao điểm AC và BD \(\Rightarrow\) I là tâm hình thoi, tọa độ I thỏa mãn:
\(\left\{{}\begin{matrix}2x-y+1=0\\x+2y-7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow I\left(1;3\right)\)
I là trung điểm AC nên tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x_C=2x_I-x_A=2\\y_C=2y_I-y_A=5\end{matrix}\right.\) \(\Rightarrow C\left(2;5\right)\)
I là trung điểm BD nên tọa độ D thỏa mãn:
\(\left\{{}\begin{matrix}x_D=2x_I-x_B=-5\\y_D=2y_I-y_B=6\end{matrix}\right.\) \(\Rightarrow D\left(-5;6\right)\)
AH
Akai Haruma
Giáo viên
30 tháng 1 2021
Lời giải:
$BD: x+2y-7=0; AD: x+3y-3=0$ nên $D$ chính là giao điểm của 2 PTĐT này.
\(\Rightarrow \left\{\begin{matrix} x_D+2y_D-7=0\\ x_D+3y_D-3=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_D=15\\ y_D=-4\end{matrix}\right.\)
Vì $ABCD$ là hình thoi nên $AC\perp BD$.
$\Rightarrow \overrightarrow{AC}=\overrightarrow{n_{BD}}=(1,2)$
$\Rightarrow \overrightarrow{n_{AC}}=(-2,1)$
PTĐT $AC$ là:
$-2(x-0)+1(y-1)=0\Leftrightarrow -2x+y-1=0\Leftrightarrow 2x-y+1=0$
Gọi $O$ là giao 2 đường chèo $AC, BD$.
\(\Rightarrow \left\{\begin{matrix} 2x_O-y_O+1=0\\ x_O+2y_O-7=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} x_O=1\\ y_O=3\end{matrix}\right.\)
$O$ là trung điểm $BD$ nên: $x_B=2x_O-x_D=2-15=-13$
$y_B=2y_O-y_D=6+4=10$
Vì $\overrightarrow{BC}=\overrightarrow{AD}$ nên PTĐT $BC$ có dạng:
$(x+13)+3(y-10)-3=0$
$\Leftrightarrow x+3y-30=0$
$O$ là trung điểm của $AC$ nên:
$x_C=2x_O-x_A=2-0=2$
$y_C=2y_C-y_A=6-1=5$
$\Rightarrow \overrightarrow{CD}=(13, -9)$
$\Rightarrow \overrightarrow{n_{CD}}=(9,13)$
PTĐT $CD$ là: $9(x-2)+13(y-5)=0\Leftrightarrow 9x+13y-83=0$
PTĐT $AB$ là: $9(x-0)+13(y-1)=0\Leftrightarrow 9x+13y-13=0$
CM
17 tháng 11 2019
Trực tâm H là giao điểm của BH và AH ⇒ tọa độ H là nghiệm của hệ:
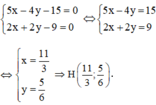
A là giao điểm của AB và AH nên tọa độ A là nghiệm của hệ phương trình:
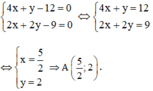
B là giao điểm BH và AB nên tọa độ điểm B là nghiệm của hệ:
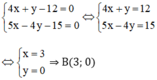
+ AC ⊥ HB, mà HB có một vtpt là (5; -4)⇒ AC nhận (4; 5) là một vtpt
AC đi qua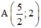 
⇒ Phương trình đường thẳng AC: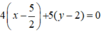 
hay 4x + 5y – 20 = 0.
+ CH ⊥ AB, AB có một vtpt là (4; 1) ⇒ CH nhận (1; -4) là một vtpt
CH đi qua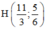 
⇒ Phương trình đường thẳng CH: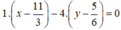 
hay CH: 3x – 12y - 1 = 0.
+ BC ⊥ AH , mà AH nhận (2; 2) là một vtpt
⇒ BC nhận (1; -1) là một vtpt
BC đi qua B(3; 0)
⇒ Phương trình đường thẳng BC: 1(x - 3) – 1(y – 0) = 0 hay x – y – 3 = 0.
CM
20 tháng 3 2018
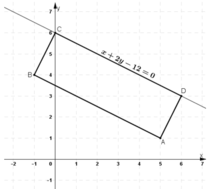
CD: x + 2y – 12 = 0 ⇒ CD nhận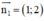 
là một vtpt
⇒ CD nhận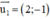 
là một vtcp.
+ ABCD là hcn ⇒ AD ⊥ CD ⇒ AD nhận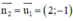 
là một vtpt
A(5 ; 1) ∈ AD
⇒ Phương trình đường thẳng AD: 2( x- 5) – 1(y – 1) = 0 hay 2x – y – 9 = 0.
+ ABCD là hcn ⇒ AB // CD ⇒ AB nhận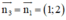 
là một vtpt
A(5;1) ∈ AB
⇒ Phương trình đường thẳng AB: 1( x- 5) + 2(y -1) = 0 hay x + 2y – 7 = 0
+ ABCD là hcn ⇒ BC ⊥ CD ⇒ BC nhận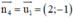 
là một vtpt
C(0, 6) ∈ CD
⇒ Phương trình đường thẳng BC: 2(x- 0)- 1(y – 6) =0 hay 2x – y + 6 = 0.
DK
1 tháng 6 2021
Để phương trình có nghiệm
\(\Delta'=\left(-m\right)^2-1.\left(m^2-\dfrac{1}{2}\right)\ge0\Leftrightarrow\dfrac{1}{2}\ge0\) ( luôn đúng)
Áp dụng vi.et có
\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2-\dfrac{1}{2}\end{matrix}\right.\)
Theo bài ra ta có
\(x_1^2+x_2^2=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=9\)
\(\Leftrightarrow\left(2m\right)^2-2\left(m^2-\dfrac{1}{2}\right)=9\)
\(\Leftrightarrow4m^2-2m^2+1=9\)
\(\Leftrightarrow2m^2=8\Leftrightarrow m^2=4\Leftrightarrow m=\pm2\)
BN
1 tháng 6 2021
Để pt có nghiệm <=> \(\Delta'\ge0\Leftrightarrow\left(-m\right)^2-1\left(m^2-\dfrac{1}{2}\right)\ge0\)
\(\Leftrightarrow m^2-m^2+\dfrac{1}{2}\ge0\Leftrightarrow\dfrac{1}{2}\ge0\) (Đúng)
Vậy pt luôn có 2 nghiệm x1,x2
Theo hệ thức vi-et, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2-\dfrac{1}{2}\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=3^2=9\)
<=>\(\left(x_1+x_2\right)^2-2x_1x_2=9\)
<=>(2m)2-2(m2-1/2)=9
<=>4m2-2m2+1=9
<=>2m2=8<=>m2=4<=>\(m=\pm2\)
cạnh thứ ba 2x-5y+3=0. cạnh thứ tư 2x-5y-26=0, đường chéo thứ hai 7x-3x-33=0