cho góc nhọn xOy; trên tia Ox lấy A(A#O); trên tia Oy lấy điểm B (B # O)sao cho OA = OB; kẻ ACvuông góc với OY (CE Oy) ; BD vuông góc Ox ( D E Ox); I là giao diểm của AC và BD
a. chứng minh tam giác AOC= tam giác BOD
b. So sánh IC và IA
c. Chứng minh tam giác AIB cân
d. Chứng minh góc IAB=M góc 1\2 góc AOB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
27 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
S
2 tháng 9 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
CM
3 tháng 4 2018
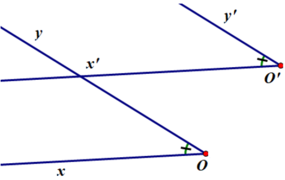
- Từ O’ vẽ O’x’ // Ox
- Từ O’ vẽ O’y’//Oy sao cho góc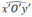 
là góc nhọn.
Ta được trường hợp hình vẽ trên
MT
1
KT
1 tháng 8 2018
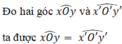
a)Ta có vì Ox song song với Ox'
Oy song song với Oy'
xOy song song với x'O'y'(Ox song song với Ox';Oy song song với Oy')
Mà theo tính chất thì nếu hai góc cùng song song với nhau thì hai góc đó bằng nhau.(cùng góc tù,goc vuông,góc nhọn)
Từ tính chất trên ta có xOy(nhọn)=x'Oy'(nhọn)
xOy(tù)=x'Oy'(tù)
Vì dù nhọn hay tù nhưng chúng song song với nhau thì chúng đều bằng nhau.(cùng góc tù,goc vuông,góc nhọn)
b)Vì ở đay khó vẽ hình nên ta có thể lý luận câu sau như sau:
Ta có xOy(sao cho ở trên) là góc nhọn,kéo dài Oy ra ta được hai góc kề bù=180o180o
Ta thấy góc được tạo kéo dài(góc tù) lại song song với x'Oy'
Vì nếu hai góc cùng song song với nhau thì hai góc đó bằng nhau.
nên x'Oy'=góc được tạo mà
xOy+góc được tạo=180o180o{x'Oy'(tù) vì bằng góc được tạo(tù)}
hay xOy+x'Oy'=180o180o(
\RightarrowxOy(nhọn)+x'Oy'(tù)=180o180o
Đáp số:a) xOy(nhọn)=x'Oy'(nhọn)
xOy(tù)=x'Oy'(tù)
Vì dù nhọn hay tù nhưng chúng song song với nhau thì chúng đều bằng nhau.
b)xOy(nhọn)+x'Oy'(tù)=180o180o
B1
12 tháng 9 2017
Cách vẽ:
- Từ O' vẽ O'x' //Ox.
- Từ O' Vẽ O'y' //Oy sao cho góc ˆx′O′y′x′O′y′^ là góc nhọn. Ta được hai trường hợp hình vẽ sau:
Đo hai góc ˆxOyxOy^ và ˆx′O′y′x′O′y′^ ta được ˆxOy=ˆx′O′y′.
Xem thêm tại: http://loigiaihay.com/bai-29-trang-92-sgk-toan-7-tap-1-c42a3297.html#ixzz4sT9fRXPl
12 tháng 9 2017
x'
Nếu O'y' không trùng với Oy thì xOy = x'O'y'(vìOy//O'y';Ox//O'x')
=> xOy =x'O'y'
DA
2
a)Xét tam giác AOC và tam giác BOD(đều là vuông)
OI là cạnh chung
OA=OB(gt)
\(\Rightarrow\) tam giác AOC= tam giác BOD(cạnh huyền cạnh góc vuông)
b)Vì tam giác AOC= tam giác BOD(cạnh huyền cạnh góc vuông)
\(\Rightarrow\)IA=IB(cặp cạnh tương ứng)
Mà IC<IB(cạnh góc vuông nhỏ hon cạnh huyền)
Do đó IC<IA
c)Vì IA=IB(CMT)
\(\Rightarrow\)tam giác AIB cân tại A
d)(mk ko hiểu bạn ghi gì cả)
câu d: chứng minh góc IAB bằng một phần hai góc AOB