Trên mặt nước nằm ngang, tại hai điểm A; B cách nhau 8,2 cm, người ta đặt hai nguồn sóng kết hợp, dao động điều hoà theo phương thẳng đứng có tần số 15 Hz và luôn dao động đồng pha. Biết tốc độ truyền sóng trên mặt nước là 30 cm/s, coi biên độ sóng không đổi khi truyền đi. Tính số điểm dao động với biên độ cực đại, cực tiểu trên đoạn AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
+ Để tại trung điểm AB, phần tử nước dao động cực đại → hai nguồn sóng cùng pha

Đáp án B
Ta có:
![]()
Tại trung điểm M của AB thì:
![]()
![]()
Vì tại M phần tử nước dao động với biên độ cực đại nên:
![]() và
và ![]()
![]() Hai nguồn sóng tại A và B dao động cùng pha nhau
Hai nguồn sóng tại A và B dao động cùng pha nhau

Chọn B.
Hai nguồn kết hợp cùng pha thì trung điểm là cực đại.

Đáp án D
+ Để tại trung điểm AB, phần tử nước dao động cực đại → hai nguồn sóng cùng pha

Đáp án C
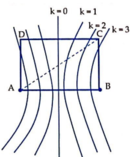
Từ hình vẽ ta thấy để trên CD có 5 điểm dao động với biên độ cực đại thì điểm C phải nằm giữa đường cực đại bậc 2 và đường cực đại bậc 3.
![]()
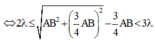
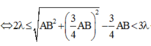
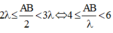
 giá trị lớn nhất là 5.
giá trị lớn nhất là 5.
Suy ra, số cực đại tối đa trên AB là 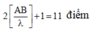

Đáp án C
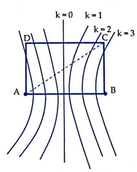
Từ hình vẽ ta thấy để trên CD có 5 điểm dao động với biên độ cực đại thì điểm C phải nằm giữa đường cực đại bậc 2 và đường cực đại bậc 3
⇒ 2 λ ≤ A C − B C < 3 λ ⇔ 2 λ ≤ A B 2 + B C 2 − B C < 3 λ ⇔ 2 λ ≤ A B 2 + 3 4 A B 2 − 3 4 A B < 3 λ ⇔ 2 λ ≤ A B 2 + 3 4 A B 2 − 3 4 A B < 3 λ ⇔ 2 λ ≤ A B 2 < 3 λ ⇔ 4 ≤ A B λ < 6
Vậy A B λ (phần nguyên của A B λ ) giá trị lớn nhất là 5
Suy ra, số cực đại tối đa trên AB là 2 A B λ + 1 = 11 đ i ể m

Đáp án C
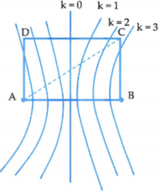
Từ hình vẽ ta thấy để trên CD có 5 điểm dao động với biên độ cực đại thì điểm C phải nằm giữa đường cực đại bậc 2 và đường cực đại bậc 3.
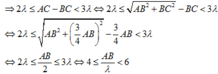
Vậy A B λ (phần nguyên của A B λ ) nhận giá trị lớn nhất là 5.
Suy ra, số cực đại tối đa trên AB là 2 A B λ +1=11 điểm.
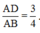
\(\lambda=\frac{v}{f}=\frac{30}{15}=2cm\)
Vì 2 nguồn cùng pha nên số điểm dao động với biên độ cực đại trên đoạn AB thỏa mãn:
\(-AB< k\lambda< AB\)
\(\Leftrightarrow\) -8,2 < 2k < 8,2
\(k\in Z\Rightarrow k=0;^+_-1;^+_-2;^+_-3;^+_-4\)
Vậy có 9 điểm dao động với biên độ cực đại trên đoạn AB.
Số điểm dao động với biên độ cực tiểu trên đoạn AB thỏa mãn:
\(-AB< \left(k+0,5\right)\lambda< AB\)
\(\Leftrightarrow\) -8,2 < (k+0,5).2 < 8,2
\(\Leftrightarrow\) -4,6 < k < 3,6
\(k\in Z\Rightarrow k=0;^+_-1;^+_-2;^+_-3;-4\)
Vậy có 8 điểm có biên độ dao động cực tiểu trên đoạn AB.