Cho tam giác ABC cân (AB = AC), có cạnh đáy BC, đường cao AH, cạnh bên AB theo thứ tự đó lập thành một cấp số nhân. Hãy tính công bội q của cấp số nhân đó ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 11 2018
Theo giả thiết AB=AC, BC,AH,AB lập thành cấp số nhân nên ta có hệ:
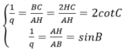
Từ đó ta có kết quả sau: 2cotC = sinC ⇔ 2cosC =sin2C = 1-cos2C
⇔ cos2C + 2cosC -1 =0 ⇒cosC = -1 +√2 (0° < C < 90°)
Do C là góc nhọn nên :
Cho nên công bội của cấp số nhân là:
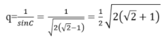
Đáp án C.
CM
16 tháng 8 2018
Đáp án B
Theo giả thiết AB = AC và BC, AH, AB theo thứ tự lập thành một cấp số nhân nên ta có hệ
CM
8 tháng 5 2018
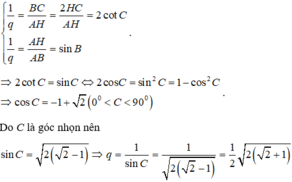
Đáp án A
Theo giả thiết AB = AC và BC, AH, AB theo thứ tự lập thành một cấp số nhân nên ta có hệ
⇒ 2 c o t C = sin C
⇔ 2 cos C = sin 2 C
Do C là góc nhọn nên sin C = 2 ( 2 - 1 )
⇒ q = 1 2 2 ( 2 - 1 )
CM
19 tháng 8 2019
Đáp án A
Theo giả thiết và BC, AH, AB theo thứ tự lập thành một cấp số nhân nên ta có hệ
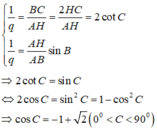
Do C là góc nhọn nên
CM
14 tháng 9 2018
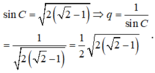
Đáp án B
Ta có
A M 2 + B C 2 2 = A B 2 B C . A B = A M 2 ⇒ B C . A B + B C 2 2 = A B 2 ⇔ A B B C 2 − A B B C − 1 4 = 0
⇔ q 2 = A B B C = 1 + 2 2 ⇔ q = 1 + 2 2
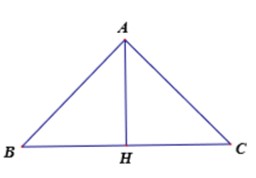
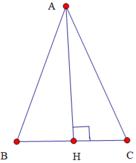
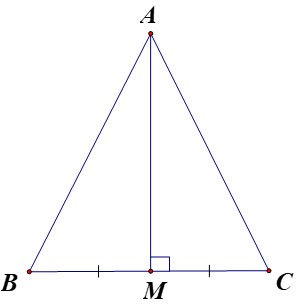
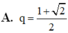
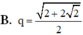
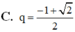
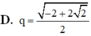
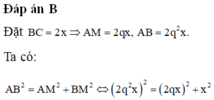
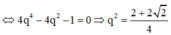
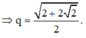
Theo giả thiết \(AB=AC,BC,AH,AB\) lập thành cấp số cộng cho nên ta có hệ :
\(\begin{cases}\frac{1}{q}=\frac{BC}{AH}=\frac{2HC}{AH}=2\cot C\\\frac{1}{q}=\frac{AH}{AB}=\sin B\end{cases}\)
Từ đó ta có kết quả :
\(2\cot C=\sin C\) hay \(2\cos C=\sin^2C=1-\cos^2C\)
\(\Leftrightarrow\cos^2C+2\cos C-1=0\)
\(\Leftrightarrow\cos C=-1+\sqrt{2}\) (0 < C < \(90^0\))
Do C là nhọn nên \(\sin C=\sqrt{2\left(\sqrt{2}-1\right)}\)
Cho nên công bội của cấp số nhân là : \(q=\frac{1}{\sin C}=\frac{1}{\sqrt{2\left(\sqrt{2}-1\right)}}=\frac{1}{2}\sqrt{2\left(\sqrt{2}-1\right)}\)