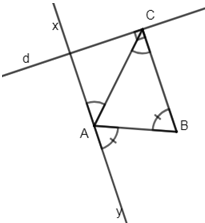
Cho tam giác ABC. trong nửa mặt phẳng bờ AB chứa C, kẻ các tia Ax và By sao cho C nằm giữa hai đường thẳng Ax và By. Chứng minh rằng
a. nếu Ax // By thì ACB = xAC + CBy.
b. Nếu ACB = xAC + Cby thì Ax // By
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 8 2023
a) Ta có: ˆCAx=ˆACB(gt)���^=���^(��) mà hai góc đó là hai góc so le trong nên
suy ra Ax//BC��//�� (1)
ˆBAy=ˆABC(gt)���^=���^(��) mà hai góc đó là hai góc so le trong nên suy ra Ay//BC��//�� (2)
Từ (1) và (2) suy ra Ax và Ay cùng // BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
⇒⇒ Ax và Ay là hai tia đối nhau.
b) Vì Ax và Ay là hai tia đối nhau (cmt) mà Ax//BC��//�� và Ay//BC��//��
nên suy ra xy//BC��//��
Mà BC⊥d��⊥� nên suy ra d⊥xy
a. Từ C kẻ đường thẳng song song với Ax và By, cắt AB tại I,
=> ACI = CAx
=> ICB = CBy
=> ACB = ACI + ICB = xAC + CBy
b. Từ C kẻ đường thẳng song song với Ax, cắt AB tại I,
=> ACI = CAx
ACB = xAC + CBy => ACI + ICB = xAC + CBy
mà ACI = CAx nên ICB = CBy => CI // By
=> Ax //By