Cho hàm số y=x3−3m2x2+m. Tìm mđể đồ thị hàm số có cực đại, cực...
Đọc tiếp
Cho hàm số y=x3−3m2x2+m. Tìm m
để đồ thị hàm số có cực đại, cực tiểu.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 3 2018
Đáp án D.
y = -x3 + (2m – 1)x2 – (2 – m)x – 2
TXĐ: D = R
y' = -3x2 + 2(2m – 1) – 2 + m
Đồ thị hàm số có cực đại và cực tiểu <=> Pt y’ = 0 có hai nghiệm phân biệt
<=> Δ’ = (2m – 1)2 + 3(-2 + m) > 0 <=> 4m2 – m – 5 > 0 <=> m ∈ (-∞; -1) ∪ (5/4; +∞)
CM
28 tháng 9 2018
Đáp án B
Ta có y ' = 3 x 2 + 3 3 a
Hàm sổ có cực trị ⇔ y ' = 0 có 2 nghiệm phân biệt ⇔ a < 0 .
Hàm số là hàm số lẻ nên đồ thị hàm số có tâm đối xứng là gốc tọa độ, do đó đường thẳng nối cực đại và cực tiểu của đồ thị hàm số luôn đi qua gốc tọa độ.
CM
5 tháng 10 2017
Chọn D
Ta có y ' = 3 x 2 - 6 m x + m - 1
Hàm số có cực đại, cực tiểu khi và chỉ khi PT y ' = 0 có hai nghiệm phân biệt
Điều này tương đương
Hai điểm cực trị có hoành độ dương
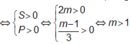
Vậy các giá trị cần tìm của m là m >1
CM
13 tháng 7 2018
Chọn A
là tam thức bậc hai có ∆' = m2.
Do đó: y có cực đại cực tiểu ⇔ y’ có hai nghiệm phân biệt
⇔ g(x) có hai nghiệm phân biệt ⇔ ∆' > 0 ⇔ m ≠ 0. (1)
Khi đó, y’ có các nghiệm là: 1 ± m
→ tọa độ các điểm cực trị của đồ thị hàm số là
Để A và B cách đều gốc tọa độ khi và chỉ khi :
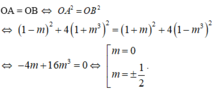
Đối chiếu với điều kiện (1), ta thấy chỉ m = ± 1 2 thỏa mãn yêu cầu bài toán.
CM
19 tháng 1 2019
Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
CM
6 tháng 2 2017
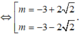
Chọn A
[Phương pháp trắc nghiệm]
y ' = 3 x 2 - 6 x - m
Hàm số có 2 cực trị m > -3 , gọi x 1 , x 2 là hai nghiệm của phương trình y ' = 0 ,
ta có: x 1 + x 2 = 2
Bấm máy tính
Hai điểm cực trị của đồ thị hàm số là
Gọi I là trung điểm của AB
⇒ I ( 1 ; - m )
Đường thẳng đi qua hai điểm cực trị là
Yêu cầu bài toán
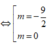
Kết hợp với điều kiện thì m = 0
Cho hàm số y=x3−3m2x2+m. Tìm m
để đồ thị hàm số có cực đại, cực tiểu.
Cho em hỏi em có được 3GP không ạ !