Cho f(x)=2/3x3+(cosa−3sina)x2−8(1+cosa)x+1
a) Chứng minh rằng hàm số luôn có cực đại và cực tiểu
b) Giả sử hàm số đạt cực trị tại x1,x2. Chứng minh rằng x12+x22≤18
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét phương trình : \(f'\left(x\right)=2x^2+2\left(\cos a-3\sin a\right)x-8\left(1+\cos2a\right)=0\)
Ta có : \(\Delta'=\left(\cos a-3\sin a\right)^2+16\left(1+\cos2a\right)=\left(\cos a-3\sin a\right)^2+32\cos^2\), \(a\ge0\) với mọi a
Nếu \(\Delta'=0\Leftrightarrow\cos a-3\sin a=\cos a=0\Leftrightarrow\sin a=\cos a\Rightarrow\sin^2a+\cos^2a=0\) (Vô lí)
Vậy \(\Delta'>0\)
với mọi a \(\Rightarrow f'\left(x\right)=0\)
có 2 nghiệm phân biệt \(x_1,x_2\) và hàm số có cực đại, cực tiểu
b) Theo Viet ta có \(x_1+x_2=3\sin a-\cos a\)
\(x_1x_2=-4\left(1+\cos2a\right)\)
\(x^2_1+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(3\sin a-\cos a\right)^2+8\left(1+\cos2a\right)=9+8\cos^2a-6\sin a\cos a\)
\(=9+9\left(\sin^2a+\cos^2a\right)-\left(3\sin a+\cos a\right)^2=18-\left(3\sin a+\cos2a\right)\le18\)

Đáp án D
Ta có:
f ' x = x 2 − 2 m + 1 x + m − 2 ⇒ Δ ' = m + 1 2 − m − 2 = m 2 + m + 3 > 0
hàm số đã cho luôn có hai cực trị tại x 1 , x 2 thõa mãn:
x 1 + x 2 = 2 m + 1 x 1 x 2 = m − 2
Ta biến đổi PT:
x 1 2 + x 2 2 = 18 ⇔ x 1 + x 2 2 − 2 x 1 x 2 = 18 ⇔ 4 m + 1 2 − 2 m − 2 = 18 ⇔ 4 m 2 + 6 m − 10 = 0 ⇔ m = 1 m = − 5 2

Đáp án A
Em có: y ' = − 3 x 2 + 6 x + 6 , Δ ' = 27 > 0.
=> Phương trình y' = 0 có 2 nghiệm phân biệt x 1 , x 2 .
Theo Vi-ét em có x 1 + x 2 = 2 x 1 x 2 = − 2 ⇒ S = x 1 2 + x 2 2 = x 1 + x 2 2 − 2 x 1 x 2 = 8.

Chọn D
D = ℝ
Phương trình y ' = 0 luôn có hai nghiệm phân biệt x 1 , x 2 và y ' đổi dấu khi x chạy qua x 1 , x 2
nên hàm số đạt cực trị tại x 1 , x 2 .
![]()
Phương pháp trắc nghiệm:
Bước 1: Giải phương trình bậc hai :
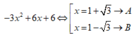
Bước 2: Tính A 2 + B 2 = 8

\(f'\left(x\right)=4x^3\Rightarrow g\left(x\right)=4x^3-3x^2-6x+1\)
\(g'\left(x\right)=12x^2-6x-6=0\Rightarrow\left[{}\begin{matrix}x_2=-\dfrac{1}{2}\\x_1=1\end{matrix}\right.\)
\(\Rightarrow g\left(-\dfrac{1}{2}\right).g\left(1\right)=\dfrac{11}{4}.\left(-4\right)=-11\)
a) Xét phương trình \(f'\left(x\right)=2x^2+2\left(\cos a-3\sin a\right)x-8\left(1+\cos2a\right)=0\)
Ta có \(\Delta'=\left(\cos a-3\sin a\right)^2+16\left(1+\cos a\right)=\left(\cos a-3\sin a\right)^2+32\cos^2a\ge0\) với mọi a
Nếu \(\Delta'=0\Leftrightarrow\cos a-3\sin a=\cos a=0\Leftrightarrow\sin a=\cos a\Rightarrow\sin^2a+\cos^2a=0\) (Vô lĩ)
Vậy \(\Delta'>0\Rightarrow f'\left(x\right)=0\) có 2 nghiệm \(x_1,x_2\) và hàm số có cực đại và cực tiểu
b) Theo Viet ta có \(x_1+x_2=3\sin a-\cos a;x_1x_2=-4\left(1+\cos2a\right)\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(3\sin a-\cos a\right)^2+8\left(1+\cos2a\right)\)
\(=9+8\cos^2a-6\sin a\cos a\)
\(=9+9\left(\sin^2a+\cos^2a\right)-\left(3\sin a+\cos a\right)^2\)
\(=18-\left(3\sin a+\cos a\right)^2\le18\)