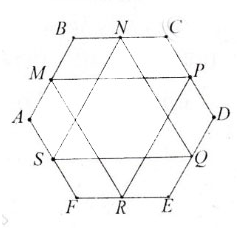
Cho ABCDEF là lục giác lồi nội tiếp đường tròn bán kính R có các cạnh AB=CA=EF=R. Chứng minh rằng trung điểm 3 cạnh BC, DE, FA là đỉnh của một tam giác đều.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 9 2018
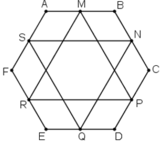
Gọi G là trọng tâm tam giác MPR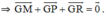 
Ta cần đi chứng minh G cũng là trọng tâm của ΔNQS bằng cách chứng minh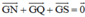 
Thật vậy ta có:
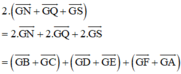
(Vì N, Q, S lần lượt là trung điểm của BC, DE, FA)
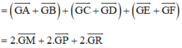
(Vì M, P, R là trung điểm AB, CD, EF)
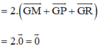
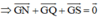hay G cũng là trọng tâm của ΔNQS.
Vậy trọng tâm ΔMPR và ΔNQS trùng nhau.
MG
13 tháng 4 2016
Ta có : =
=
=
=> +
+
=
(
+
+
) =
=
=> +
+
=
(1)
Gọi G là trong tâm của tam giác MPR, ta có:
+
+
=
(2)
Mặt khác : =
+
=
+
=
+
=> +
+
=(
+
+
)+
+
+
(3)
Từ (1),(2), (3) suy ra: +
+
=
Vậy G là trọng tâm của tam giác NQS
= 
=
= 
= 
+ 
+
= 
+
+
+
19 tháng 5 2017
Giải:
Gọi \(G\) là trọng tâm của \(\Delta MPR\) và \(K\) là trọng tâm của của \(\Delta NQS\)
\(\Rightarrow\) Ta cần chứng minh: \(K\) và \(G\) trùng nhau
Vì \(G\) là trọng tâm của \(\Delta MPR\) nên ta có:
\(3\overrightarrow{KG}=\overrightarrow{KM}+\overrightarrow{KP}+\overrightarrow{KR}\)
\(=\dfrac{1}{2}\left(\overrightarrow{KA}+\overrightarrow{KB}+\overrightarrow{KC}+\overrightarrow{KD}+\overrightarrow{KE}+\overrightarrow{KF}\right)\) (t/c trung điểm)
\(=\dfrac{1}{2}\left(\overrightarrow{KB}+\overrightarrow{KC}\right)+\dfrac{1}{2}\left(\overrightarrow{KD}+\overrightarrow{KE}\right)+\dfrac{1}{2}\left(\overrightarrow{KA}+\overrightarrow{KF}\right)\)
\(=\overrightarrow{KN}+\overrightarrow{KQ}+\overrightarrow{KS}=\overrightarrow{0}\) (Vì \(K\) là trọng tâm của của \(\Delta NQS\))
\(\Rightarrow\) Đpcm
CM
16 tháng 5 2018
a)
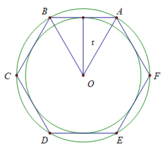
b) Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)
Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm
(Ta đã nêu được cách chia đường tròn thành sáu cung bằng nhau tại bài tập 10 SGK trang 71)
c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau ( định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây)
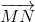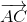
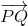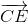
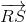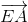
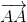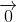
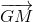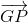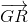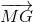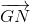
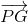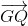
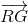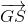
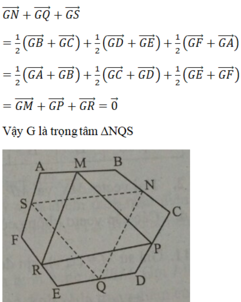
Ta cần chứng minh tam giác MNP là tam giác cân và có một góc bằng \(\frac{\Pi}{3}\)
Giả sử lục giacs có hướng âm, kí hiệu \(f\) là phép quay vec tơ theo góc \(-\frac{\Pi}{3}\) và M, N. P theo thứ tự là trung điểm FA, BC, DE
Khi đó AB=BO, CD=DO=OC, EF=FO=OE nên các tam giác ABO, CDO, EFO đều và có hướng âm
Suy ra \(f\left(\overrightarrow{AB}\right)=\overrightarrow{AO}\), \(f\left(\overrightarrow{OC}\right)=\overrightarrow{OD}\), \(f\left(\overrightarrow{FO}\right)=\overrightarrow{FE}\)
Từ đó ta có :
\(f\left(\overrightarrow{MN}\right)=f\left(\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{FC}\right)\right)=\frac{1}{2}\left(f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{FC}\right)\right)\)
\(=\frac{1}{2}\left(\overrightarrow{AO}\right)+\overrightarrow{OD}+\overrightarrow{FE}=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{FE}\right)\)
\(=\overrightarrow{MP}\)
Suy ra tam giác MNP cân và có góc PMN = \(\frac{\Pi}{3}\) => Điều phải chứng minh