Cho bốn đường thẳng: ; ; ; cắt nhau tại bốn điểm A, B, C, D. Chu vi tứ giác ABCD...
Đọc tiếp
Cho bốn đường thẳng: ;
;
;
cắt nhau tại bốn điểm A, B, C, D. Chu vi tứ giác ABCD = (đvđd)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DH
1
Những câu hỏi liên quan
7 tháng 10 2023
Tham khảo:
a,
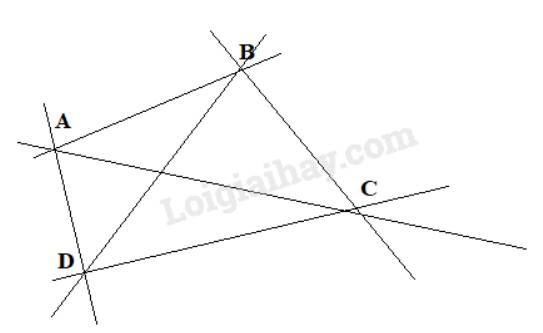
Có 6 đường thẳng đi qua hai trong bốn điểm đã cho. Đó là các đường thẳng: AB, AC, AD, BC, BD, CD.
b,
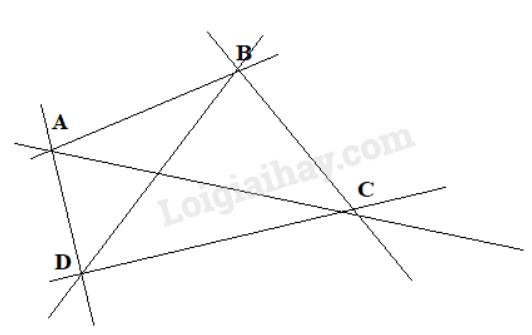
Có 12 tia với gốc là một trong bốn điểm đã cho và đi qua một trong 3 điểm còn lại. Đó là các tia: AB, BA, AC, CA, AD, DA, BC, CB, BD, DB, CD, DC.
c,
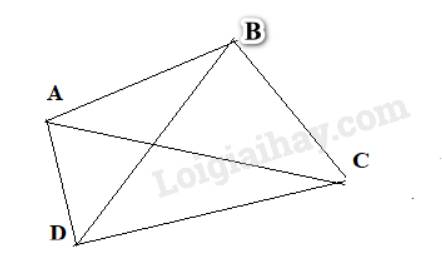
Có 6 đoạn thẳng có hai mút là hai trong bốn điểm đã cho. Đó là các đoạn thẳng: AB,AC,AD,BC,BD,CD.
21 tháng 3 2022
refer
Bốn đường thẳng a, b, c, d cắt nhau tại một điểm.
Vì giả sử ba đường thẳng a, b, c cắt nhau tại điểm A. Ta có hai đường thẳng b, c cắt nhau duy nhất tại điểm A.
Mà đường thẳng d cắt đường thẳng b và đường thẳng c tại một điểm. Nên đường thẳng d cắt đường thẳng b, c tại điểm A.
Khi đó, bốn đường thẳng a, b, c, d cùng cắt nhau tại điểm A.
21 tháng 3 2022
Tham khảo:
Bốn đường thẳng a, b, c, d cắt nhau tại một điểm.
Vì giả sử ba đường thẳng a, b, c cắt nhau tại điểm A. Ta có hai đường thẳng b, c cắt nhau duy nhất tại điểm A.
Mà đường thẳng d cắt đường thẳng b và đường thẳng c tại một điểm. Nên đường thẳng d cắt đường thẳng b, c tại điểm A.
Khi đó, bốn đường thẳng a, b, c, d cùng cắt nhau tại điểm A
CM
12 tháng 7 2017
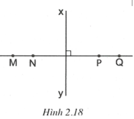
Ta có M N ⊥ x y ; P Q ⊥ x y (vì xy là đường trung trực của NP). Qua điểm N chỉ vẽ được một đường thẳng vuông góc với xy, suy ra ba điểm M, N, P thẳng hàng. (1)
Ta có N P ⊥ x y ; P Q ⊥ x y . Qua điểm P chỉ vẽ được một đường thẳng vuông góc với xy, suy ra ba điểm N, P, Q thẳng hàng. (2)
Từ (1) và (2) suy ra các điểm M, N, P, Q thẳng hàng vì chúng cùng thuộc đường thẳng NP
CM
26 tháng 4 2017
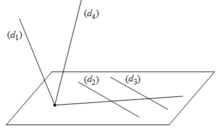
Hai đường thẳng d 1 , d 3 song song và nằm trong mặt phẳng 3y + z -6 =0.
Hai đường thẳng d 2 , d 4 phân biệt cùng cắt mặt phẳng 3y + z -6 =0. tại điểm A(4;2;0).
Qua A có vô số đường thẳng cắt Hai đường thẳng d 1 , d 3 . Vậy có vô số đương thẳng cắt bốn đường thẳng đã cho.
Đáp án B
CM
1 tháng 6 2018
Chọn D
Đường thẳng d₁ đi qua điểm M₁ = (3;-1;-1) và có một véctơ chỉ phương là 
Đường thẳng d₂ đi qua điểm M₂ = (0;0;1) và có một véctơ chỉ phương là 
Do 
và M₁ ∉ d₁ nên hai đường thẳng d₁ và d₂ song song với nhau.
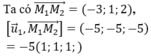
Gọi (α) là mặt phẳng chứa d₁ và d₂ khi đó (α) có một véctơ pháp tuyến là 
. Phương trình mặt phẳng (α) là x+y+z-1=0.
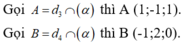
Do 
không cùng phương với 
nên đường thẳng AB cắt hai đường thẳng d₁ và d₂.
tìm tọa độ giao điểm của d1 và d2,d2 và d3, d3 và d4, d4 và d1.Có được bốn tọa độ bốn điểm thì tính từng cạnh rồi tìm chu vi