Urani ciz z = 92 A = 238 sau nhiều lần phóng xạ anpha và beeta trừ biền thành Pb ( 206) biết T của U238 = 4.6*109 gỉa sử ban đầu một loại đá chỉ chứa urani không chứa chì .nếu hiện nay tỉ lệ của các khối lượng của U/Pb = 37 thì tuổi của đá bằng bn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A.
Số hạt ![]() còn lại:
còn lại: 
Số hạt ![]() sinh ra = số hạt
sinh ra = số hạt ![]() phân rã:
phân rã:
![]()
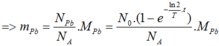
Mặt khác: 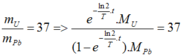

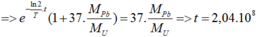 (năm).
(năm).

Tỉ lệ khối lượng chì tạo thành và khối lượng U còn lại được xác định bởi
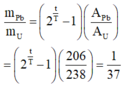
Giải phương trình trên ta thu được: t = 2 . 10 8 năm
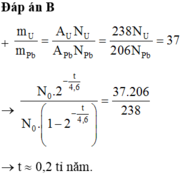
Đáp án B

Tỉ lệ các khối lượng $\dfrac{m(U)}{m(Pb)} $ bằng tỉ số các nguyên tử $\dfrac{N(U)}{N(Pb)} $nhân với tỉ số các khối, do vậy:
$\dfrac{m(U)}{m(Pb)} =\frac{N(U)}{N(Pb)}.\dfrac{238}{206} =37$
$\dfrac{N(U)}{N(Pb)}=32 $, nghĩa là hiện nay cứ 32 nguyên tử urani thì có 1 nguyên tử chì, do 1 nguyên tử urani sinh ra. Vậy ban đầu có 33 nguyên tử urani.
Ta có $32=33.2^{-t/T}$. Suy ra $2^{-t/T}=0,97$.
Vậy $t=2.10^8$ năm.
cho e hỏi tại sao lại có 1 nguyên tử Urani sinh ra ạ
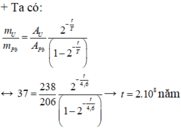
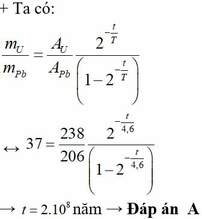

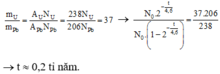
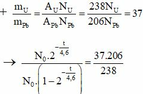
Cứ 1 hạt Urani phân rã thì tạo thành 1 hạt Pb
Như vậy số mol Unrani bị phân rã = số mol Pb tạo thành. Gọi \(\Delta m = m_0 -m(t) = m_0.2^{-t/T}\) là khối lượng urani bị phân rã.
Ta có khối lượng Pb tạo thành là
\(m_{Pb} = n_{Pb}.A_{Pb} = \frac{\Delta m_{Urani}}{A_{Ur}}.A_{Pb}. \)
Ta có tỉ lệ khối lượng Urani còn lại và khối lượng Pb sinh ra là
\(\frac{m_{Urani}}{m_{Pb}} = \frac{m_o.2^{-t/T}}{\Delta m .206/238} =\frac{238.m_o.2^{-t/T}}{\Delta m .206} = 37 \)
=> \(\frac{m_o.2^{-t/T}.238}{m_0(1-2^{-t/T}) .206} = 37. \)
=> \(238.2^{-t/T} = 7622.(1-2^{-t/T}).\)
=> t = 2,04.108 năm.
Như vậy tuổi của đã là t = 2,04.108 năm.