Đoạn sáng AB hình mũi tên đặt vuông góc với trục chính của một thấu kính mỏng quang tâm O cho ảnh A1B1 ngược chiều và cao gấp 3 lần đoạn AB (điểm A thuộc về trục chính của thấu kính).
a/ Thấu kính O thuộc loại gì? Giải thích? Vẽ hình đúng tỉ lệ vật và ảnh? b/ Nếu AB cho ảnh A2B2 ngược chiều và cao gấp 2 lần đoạn AB thì khoảng cách giữa vật và ảnh thay đổi một khoảng bằng 20cm so với vị trí ban đầu. Tìm tiêu cự thấu kính O, khoảng cách giữa vật và ảnh?Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
d = f − f k 1 d − 15 = f − f k 2 ⇒ f − d f + 15 − d = k 2 k 1 = A 2 B 2 ¯ A 1 B 1 ¯ = − 2 → f = 20 c m d = 30 c m ⇒ k 1 = − 2 k 1 = A 1 B 1 A B ⇒ A B = A 1 B 1 k 1 = 1 , 2 − 2 = 0 , 6 c m
Chú ý: Đối với thấu kính hội tụ, lúc đầu ảnh thật, lúc sau ảnh ảo nên phải dịch vật lại gần thấu kính.

a) Bạn tự vẽ hình.
b) Hình minh họa :
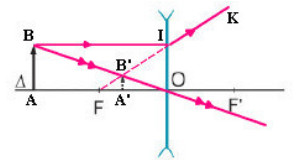
Xét \(\Delta FA'B'\sim\Delta FOI\) có : \(\dfrac{A'B'}{OI}=\dfrac{A'F}{OF}\Leftrightarrow\dfrac{A'B'}{AB}=\dfrac{OF-OA'}{OF}\)
\(\Rightarrow\dfrac{h'}{3}=\dfrac{15-d'}{15}\left(1\right)\)
Xét \(\Delta OA'B'\sim\Delta OAB\) có : \(\dfrac{A'B'}{AB}=\dfrac{OB'}{OB}\Leftrightarrow\dfrac{h'}{3}=\dfrac{d'}{30}\left(2\right)\).
Từ (1) và (2), ta có hệ phương trình : \(\left\{{}\begin{matrix}\dfrac{h'}{3}=\dfrac{15-d'}{15}\\\dfrac{h'}{3}=\dfrac{d'}{30}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d'=10\left(cm\right)\\h'=1\left(cm\right)\end{matrix}\right.\).
Vậy : Ảnh A'B' cách thấu kính \(d'=10\left(cm\right)\) và cao \(h'=1\left(cm\right)\).
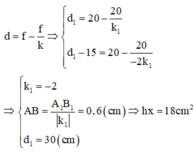
Giải:
a) Dựa vào tính chất và độ lớn của vật và ảnh thì đây là ảnh được tạo bởi thấu kính hội tụ. Vì thấu kính hội tụ cho cả ảnh ảo và ảnh thật. + Ảnh ảo> vật+ Ảnh thật có thể lớn hơn, bằng và nhỏ hơn vật Nhưng đối với thấu kính phân kỳ chỉ cho ảnh ảo và nhỏ hơn vật Để ảnh cao gấp 3 lần vật thì vật phải được đặt trong đoạn FI (ngoài khoảng tiêu cự của thấu kính). Hình vẽ minh họa ởdưới
b) Hình ảnh phía trên. Tiêu cự: 1/f = 1/d + 1/d' (1)Hệ số phóng đại: k= -d'/d = -2. suy ra được d' = 2d (2)khoảng cách giữa vật và ảnh: d + d' = L (3)So sánh với khoảng cách ban đầu thì ta thấy 0,75f = 20 cm. Từ đây suy ra được f. Có f ta thế vào (1) và (2) để tìm d và d'. Cuối cùng thế giá trị vào (3) để có được khoảng cách giữa vật và ảnh.b