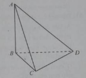
Mọi nguời ơi giúp mình bài này với ạ
Cho hình tứ diện ABCD có ba cạnh AB. BC, BD đôi một vuông góc
1. Chứng minh AB vuông góc mp (ABC)
2. Chứng minh AB vuông góc cạnh CD
3. Chứng minh BC vuông góc mp (ABD)
4.Chứng minh BD vuông góc mp (ABC)
5. chứng minh mp(ABC) vuông góc mp(ABD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

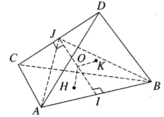
Gọi I và J lần lượt là trung điểm của AB và CD. Vì ΔACD = ΔBDC nên các tiếp tuyến tương ứng của chúng bằng nhau, do đó AJ = BJ. Từ đó suy ra IJ ⊥ AB. Tương tự, IJ ⊥ CD. Vậy IJ là đường vuông góc chung của AB và CD.
Làm tương tự đối với các cặp cạnh đối diện khác ta chứng minh được rằng đường nối trung điểm của các cặp cạnh đối diện là đường vuông góc chung của cặp cạnh đó. Do đó các đường đó đồng quy tại O là trung điểm của mỗi đường.
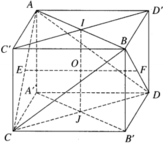
Gọi (P) là mặt phẳng qua AB và song song với CD, (Q) là mặt phẳng qua CD và song song với AB; A', B' lần lượt là hình chiếu vuông góc của A, B lên (Q); C', D' lần lượt là hình chiếu vuông góc của C, D lên (P). Dễ thấy AC'BD'.A'CB'D là hình hộp chữ nhật. Đường nối hai tâm của mỗi cặp mặt đối diện của hình hộp chữ nhật đó chính là đường vuông góc chung của các cặp cạnh đối diện của tứ diện ABCD. Do đó chúng đôi một vuông góc với nhau.

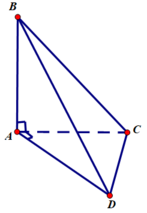
AB ⊥ AC, AB ⊥ AD nên AB ⊥ (AC, AD) hay AB ⊥ (ACD) (theo định lí trang 99)
AB ⊂ (ABC) nên (ABC) ⊥ (ACD) (theo định lí 1 trang 108)
AB ⊂ (ADB) nên (ADB) ⊥ (ACD)
AD ⊥ AC, AD ⊥ AB nên AD ⊥ (AC, AB) hay AD ⊥ (ABC)
AD ⊂ (ADB) nên (ADB) ⊥ (ABC)