Tính diện tích hình phẳng (H) y=sin2x.cos3x , y=0 ,x=0 , x=pi/2

TH

Thư Hoàngg

2 tháng 3 2016

Câu hỏi hay

Tính diện tích hình phẳng (H) y=sin²x.cos³x , y=0 ,x=0 , x=pi/2

#Toán lớp 12

1

LD

Lương Đức Trọng

2 tháng 3 2016

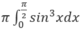
$I=\int_0^{\pi/2}\sin^2 x.cos^3 xdx=\int_0^{\pi/2}\sin^2 x.(1-\sin^2 x)d(\sin x)=\dfrac{\sin^3 x}{3}\Big|_0^{\pi/2}-\dfrac{\sin^5 x}{5}\Big|_0^{\pi/2}=\dfrac{2}{15}$

Do đó diện tích hình phẳng là $S=|I|=\dfrac{2}{15}$

Đúng(0)

SG

Sách Giáo Khoa

1 tháng 4 2017

Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox :

a) $y=1-x^2;y=0$

b) $y=\cos x;y=0;x=0;x=\pi$

c) $y=\tan x;y=0;x=0;x=\dfrac{\pi}{4}$

#Toán lớp 12

1

HB

Hai Binh

11 tháng 4 2017

a) Phương trình hoành độ giao điểm

1 - x² = 0 ⇔ x = ±1.

Thể tích cần tìm là :

$V=\frac{-1}{1}(1-x^{2})^{2}dx=2\pi \int_{0}^{1}(x^{4}-2x^{2}+1)dx$

$=2\pi \left (\frac{x^{4}}{5}- \frac{2}{3}x^{3}+x \right )|_{0}^{1}=2\pi\left ( \frac{1}{5}-\frac{2}{3}+1 \right )=\frac{16}{15}\pi$

b) Thể tích cần tìm là :

$V= \pi \int_{0}^{\pi }cos^{2}xdx =\frac{\pi }{2}\int_{0}^{\pi}(1+cos2x)dx$

$=\frac{\pi }{2}\left (x+\frac{1}{2}sin2x \right )|_{0}^{\pi }=\frac{\pi }{2}\pi =\frac{\pi ^{2}}{2}$

c) Thể tích cần tìm là :

$V=\int_{0}^{\frac{\pi }{4}}tan^{2}xdx=\int_{0}^{\frac{\pi }{4} }\left (\frac{1}{cos^{2}x}-1 \right )dx$

$=\pi \left (tanx-x \right )|_{0}^{\frac{\pi }{4}}=\pi (1-\frac{\pi }{4})$ .

Đúng(0)

PT

Pham Trong Bach

7 tháng 12 2017

Tính diện tích hình phẳng giới hạn bởi:

y = x , y = x - 2 , y = 0

A. 3

B. 10

C. 10 3

D. 3 10

#Mẫu giáo

1

CM

Cao Minh Tâm

7 tháng 12 2017

Đáp án đúng : C

Đúng(0)

PT

Pham Trong Bach

20 tháng 6 2017

Tính diện tích hình phẳng giới hạn bởi: y = x , y = x - 2 , y = 0 A. 3 B. 10 C. 10 3 D. 3 10 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

20 tháng 6 2017

Đáp án C.

Đúng(0)

SG

Sách Giáo Khoa

14 tháng 4 2017

Tính thể tích của vật thể tròn xoay khi các hình phẳng giới hạn bởi các đường sau quanh trục Ox :

a) $y=x^3;y=1;x=3$

b) $y=\dfrac{2}{\pi}x;y=\sin x;x\in\left[0;\dfrac{\pi}{2}\right]$

c) $y=x^{\alpha};\alpha\in\mathbb{N}^{\circledast};y=0;x=0;x=1$

#Toán lớp 12

0

SG

Sách Giáo Khoa

14 tháng 4 2017

Tính thể tích của vật thể tròn xoay khi các hình phẳng giới hạn bởi các đường sau quanh trục Ox :

a) $y=x^3;y=1;x=3$

b) $y=\dfrac{2}{\pi}x;y=\sin x;x\in\left[0;\dfrac{\pi}{2}\right]$

c) $y=x^{\alpha};\alpha\in\mathbb{N}^{\circledast};y=0;x=0;x=1$

#Toán lớp 12

0

PT

Pham Trong Bach

14 tháng 2 2019

Tính diện tích S của hình phẳng giới hạn bởi các đường y = e x , y = 2 , x = 0 , x = 1 . A. S = 4 ln 2 + e - 5 B. S = 4 ln 2 + e - 6 C. S = e 2 - 7 D. S = e - 3 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

14 tháng 2 2019

Đúng(0)

PT

Pham Trong Bach

19 tháng 3 2019

Tính diện tích S của hình phẳng giới hạn bởi các đường y = e x , y = 2 , x = 0 và x = 1.

A. S = 4 ln 2 + e - 5

B. S = 4 ln 2 + e - 6

C. S = e 2 - 7

D. S = e - 3

#Mẫu giáo

1

CM

Cao Minh Tâm

19 tháng 3 2019

Đáp án A

Phương trình hoành độ giao điểm e x = 2 ⇔ x = ln 2

Suy ra diện tích cần tìm bằng S = ∫ 0 ln 2 e x - 2 d x + ∫ ln 2 0 e x - 2 d x = 4 ln 2 + e - 5 .

Đúng(0)

PT

Pham Trong Bach

4 tháng 9 2018

Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng

A. S/4.

B. 4S.

C. 2S.

D. S/2.

#Mẫu giáo

1