Catôt của một tế bào quang điện làm bằng chất có giới hạn quang điện là \(0,0657\mu m\).
1) Tìm công thoát của êlectron ra khỏi bề mặt catôt
2) Tìm vận tốc ban cực đại của electron khi chiếu vào catôt ánh sáng có bước sóng \(\text{λ=0,444μm}\).
3) Tìm hiệu điện thế hãm để không có electron về catôt.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu hỏi của bn có ở đây nhá Câu hỏi của HOC24 - Học và thi online với HOC24

- Năng lượng photon của bức xạ λ1:
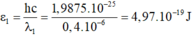
- Năng lượng photon của bức xạ λ2:
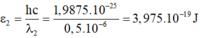
- Ta có:
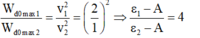
- Thay ε1 và ε2 vào phương trình trên ta được:
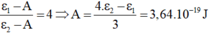
→ Giới hạn quang điện của kim loại trên:
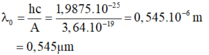

Đáp án A
+ Năng lượng photon của bức xạ λ 1 : ε 1 = hc λ 1 = 1 , 9875 .10 − 25 0 , 4 .10 − 6 = 4 , 97 .10 − 19 J
+ Năng lượng photon của bức xạ λ 2 : ε 2 = hc λ 2 = 1 , 9875 .10 − 25 0 , 5 .10 − 6 = 3 , 975 .10 − 19 J
+ Ta có: W d 0 max 1 W d 0 max 2 = v 1 2 v 2 2 = 2 1 2 ⇒ ε 1 − A ε 2 − A = 4
+ Thay ε 1 và ε 2 vào phương trình trên ta được: ε 1 − A ε 2 − A = 4 ⇒ A = 4 . ε 2 − ε 1 3 = 3 , 64 .10 − 19 J
+ Giới hạn quang điện của kim loại trên: λ 0 = hc A = 1 , 9875 .10 − 25 3 , 64 .10 − 19 = 0 , 545 .10 − 6 m = 0 , 545 μm

Đáp án D
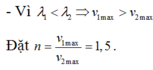
- Theo công thức Anh-xtanh, ta có:
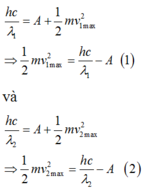
- Lấy (1) chia (2) vế theo vế:
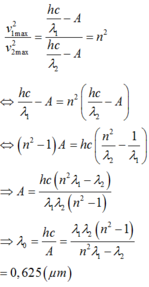

Đáp án B
Phương pháp: Công thức Anh – xtanh 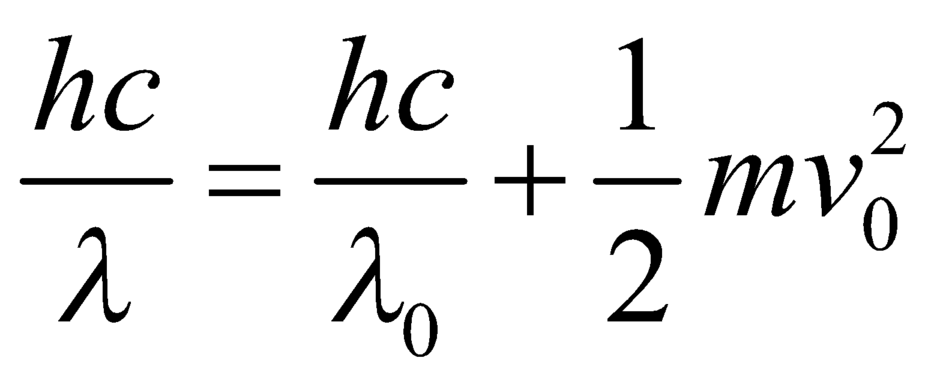
Cách giải:
Ta có:
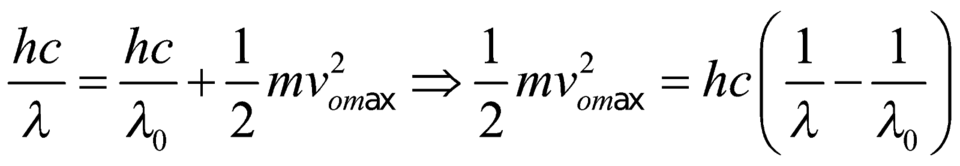
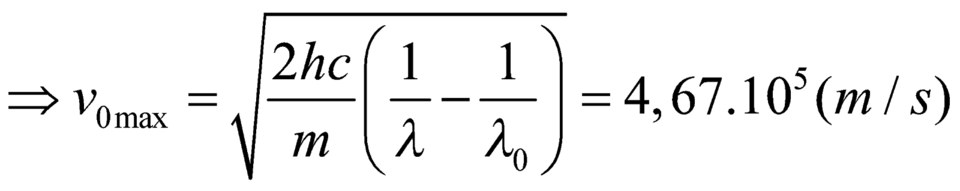

Đáp án B
Phương pháp: Công thức Anh – xtanh h c λ = h c λ 0 + 1 2 m v 0 2
Cách giải: Ta có:
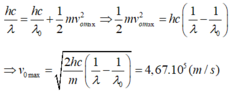

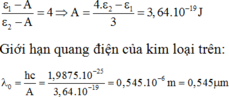



1) Công thoát của êlectron ra khỏi bề mặt catôt
\(A=\frac{hc}{\lambda_0}=3,025.10^{-19}J\)
2) Vận tốc ban cực đại của electron
\(V_{max}=\sqrt{\frac{2hc}{m}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)}=5,6.10^5m\text{/}s\)
3) Hiệu điện thế hãm để không có electron về catôt.
\(v_h=\frac{hc}{e}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)=0,91V\)