Cho đa thức: P(x) = ax4 + bx3 + cx2 + dx + e nguyên với mọi x
C/M : a, b, c, d, e nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
\(M=6x^2+xyz+2xy+3-y^2+3xyz-5x^2+7xy-9\)
\(=x^2+4xyz+9xy-y^2-6\)

Bài 2:
a: Sửa đề: \(x^2+2x+3\)
Đặt \(x^2+2x+3=0\)
\(\Delta=2^2-4\cdot1\cdot3=4-12=-8< 0\)
Do đó: Phương trình vô nghiệm
b: Đặt \(x^2+4x+6=0\)
\(\Leftrightarrow x^2+4x+4+2=0\)
\(\Leftrightarrow\left(x+2\right)^2+2=0\)(vô lý)

Ta có
![]()
Đồ thị hàm số ![]() cắt trục hoành tại bốn điểm phân biệt bên phương trình
cắt trục hoành tại bốn điểm phân biệt bên phương trình ![]() , với
, với ![]() là các nghiệm.
là các nghiệm.
Suy ra
![]()
![]()
![]()
![]()
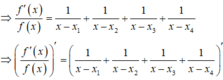
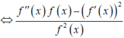
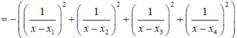
Nếu ![]() với
với ![]() thì
thì ![]() ,
, ![]()
![]() .
.
Nếu ![]() thì
thì 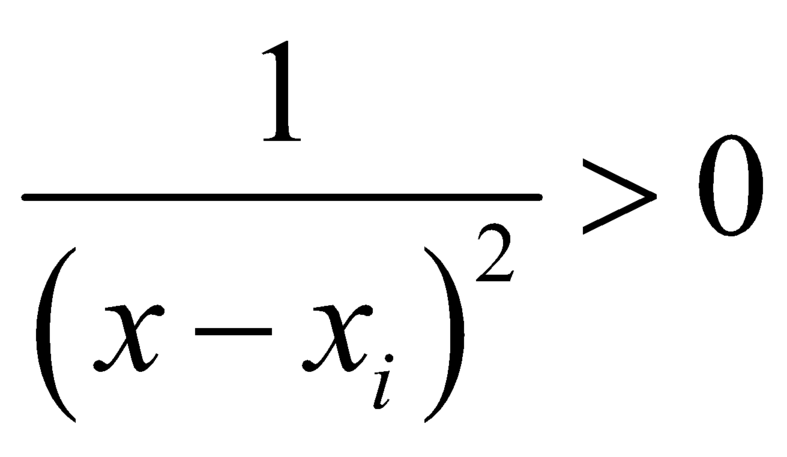 ,
, ![]() .
.
Suy ra ![]()
![]() .
.
Vậy phương trình ![]() vô nghiệm hay phương trình
vô nghiệm hay phương trình ![]() vô nghiệm.
vô nghiệm.
Do đó, số giao điểm của đồ thị hàm số và trục hoành là 0
Đáp án A

Chọn C
Ta có: ![]()
Dựa vào đồ thị:
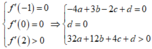

![]()
Dựa vào đồ thị, ta cũng có: ![]()
Từ (1),(2) suy ra a + c > 4a + c > 0.

Từ đồ thị hàm số (C): y = f(x) ta suy ra đồ thị hàm số (C'): y = f(|x|) như sau:
+) Giữ nguyên phần đồ thị (C) trên miền x ≥ 0 , (kí hiệu phần đồ thị này là C 1 ).
+) Bỏ phần đồ thị (C) ở bên trái trục Oy.
+) Lấy đối xứng C 1 qua trục Oy, (kí hiệu phần đồ thị này là C 2 ).
Khi đó đồ thị của hàm số y = f(|x|) là hợp của hai phần đồ thị C 1 và C 2 .
Ta có đồ thị của hàm số y = f(|x|) như hình vẽ dưới đây:
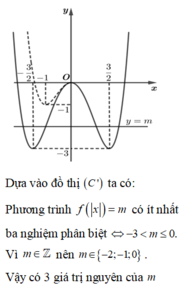
Chọn C

Đáp án B
Giả thiết
![]()
Đặt
![]()
thì
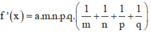
Và
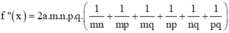
Khi đó, phương trình
![]() (vô nghiệm)
(vô nghiệm)
Vậy đồ thị hàm số y = g(x) không cắt trục hoành.